Условие задачи (1978, № 10) Задача М530 // Квант. — 1978. — № 10. — Стр. 39; 1979. — № 10. — Стр. 28—29.
На прямоугольном листе бумаги в клетку некоторые клетки закрашены в чёрный цвет. Затем происходит одновременное перекрашивание всех клеток листа по следующему правилу: клетка, имевшая чётное число чёрных соседей, становится белой, а имевшая нечётное число чёрных соседей — чёрной. (Соседями считаются клетки, имеющие общую сторону.)
- Докажите, что если множество
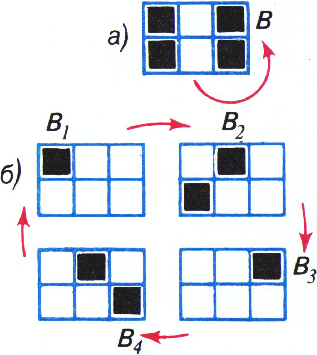
$B$ чёрных клеток при перекрашивании не изменяется (рис. 1, а), то в$B$ чётное число клеток. - Пусть при перекрашивании множество
$B_1$ чёрных клеток переходит в$B_2$, $B_2$ — в$B_3$, $\ldots$, $B_{r-1}$ — в$B_r$, а$B_r$ — снова в$B_1$ (рис. 1, б). Докажите, что общее число чёрных клеток в множествах$B_1$, $B_2$, $\ldots$, $B_r$ чётно.
Изображения страниц
Решение задачи (1979, № 10) Задача М530 // Квант. — 1978. — № 10. — Стр. 39; 1979. — № 10. — Стр. 28—29.
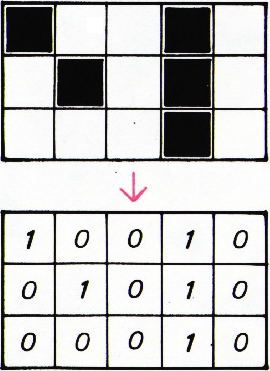
Заменим наш лист бумаги таблицей из нулей и единиц: если клетка чёрная, напишем на её месте единицу, а если белая — ноль (рис. 2). Определим для каждой клетки сумму её соседей «по модулю 2», т. е. по следующему правилу: $$ \begin{gather*} 0+0=1+1=0;\\ 1+0=0+1=1.\\ \end{gather*} $$
Сумму соседей данной клетки назовём её ореолом, а вместо слов «чёрная клетка» будем писать «1-клетка».
Из условия задачи следует, что состояние клетки (т. е. записанное в ней число) в некоторый момент времени равно её ореолу в предыдущий момент.
а) Если множество
б) Будем писать
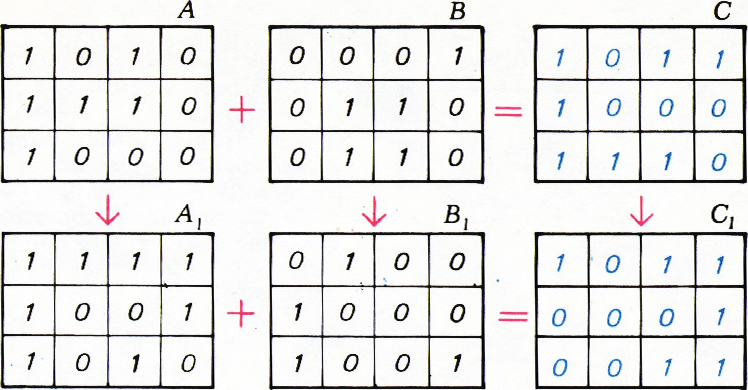
Лемма. Если
Это следует из того, что при сложении ореолы клеток тоже складываются.
Приступим к решению задачи б). Пусть $$ B_1\to B_2\to\ldots\to B_r\to B_1. $$ Используя лемму, получаем: $$ \begin{gather*} B_1+B_2\to B_2+B_3\to\ldots\to B_r+B_{1}\to B_1+B_2,\\ B_1+B_2+B_3\to B_2+B_3+B_4\to\ldots\to B_r+B_1+B_2\to B_1+B_2+B_3,\\ .~~.~~.~~.~~.~~.~~.~~.~~.~~.~~.~~.~~.~~.~~.~~.~~.~~.~~.~~.~~.~~.\\ B_1+B_2+B_3+\ldots+B_r\to B_1+B_2+B_3+\ldots+B_r. \end{gather*}$$
Из последней строчки и задачи а) следует, что в таблице
Задача М530 решена. Но в связи с ней возникает много интересных вопросов. Например, чему может равняться


