Условие задачи (1978, № 10) Задача М528 // Квант. — 1978. — № 10. — Стр. 38—39; 1979. — № 9. — Стр. 24.
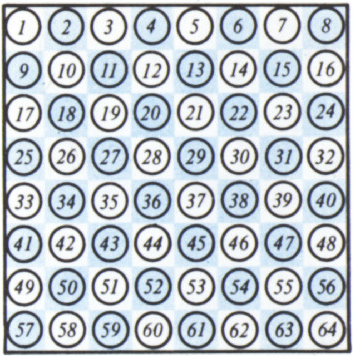
На каждой клетке шахматной доски стоит по фишке (рис. 1). Фишки нужно переставить так, чтобы расстояние между каждой парой фишек не уменьшилось по сравнению с расстоянием между ними при первоначальном расположении. Сколькими способами это можно сделать? (Расстоянием между фишками считается расстояние между центрами клеток, которые они занимают.)
Изображения страниц
Решение задачи (1979, № 9) Задача М528 // Квант. — 1978. — № 10. — Стр. 38—39; 1979. — № 9. — Стр. 24.
Докажем, прежде всего, что требуемая перестановка фишек сохраняет расстояния между любыми двумя фишками. Это можно сделать многими разными способами.
Первый способ. Сумма всех попарных расстояний между фишками не изменяется. Отсюда следует, что ни одно из расстояний не может увеличиться (действительно, если после перестановки фишек расстояние между какими-либо фишками увеличится, то, поскольку сумма всех расстояний постоянна, найдутся фишки, расстояние между которыми уменьшится, что противоречит условию перестановки).
Второй способ. Угловые фишки
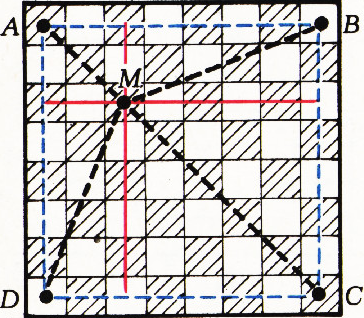
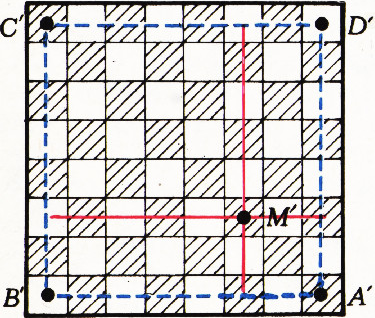
Из наших доказательств ясно, что нужная перестановка фишек определяет некоторое перемещение квадрата
Заметим, что основной результат задачи допускает такое красивое обобщение: если


