Задача М523‍‍

а) Пусть $n$‍‍ нечётно. В этом случае доску размером $n\times n$‍,‍ кроме углового поля, можно покрыть костями домино $2\times1$‍‍ (рис. 2, а). Пусть тот, кто ходит вторым, следует такой стратегии: ставит фишку на второе поле того домино, на первое поле которого поставил фишку начинающий игру. Ясно, что, поступая таким сбразом, второй игрок выиграет.

Пусть $n$‍‍ чётно. Тогда доску размером $n\times n$‍‍ можно покрыть костями домино целиком (рис. 2, б). В этом случае начинающий игрок, считая, что «нулевым» ходом его партнёр поставил фишку на угловое поле доски, должен следовать описанной выше стратегии второго игрока. Ясно, что теперь победит начинающий игру.

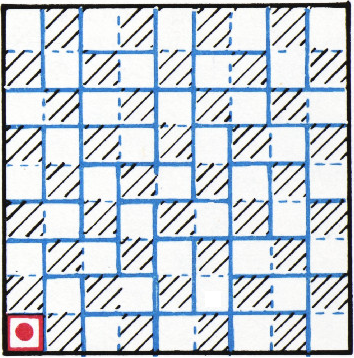
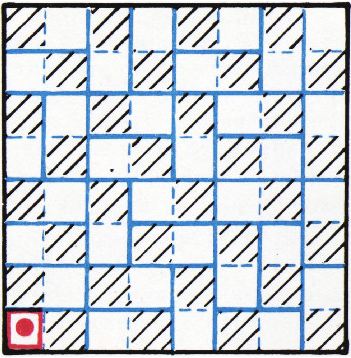
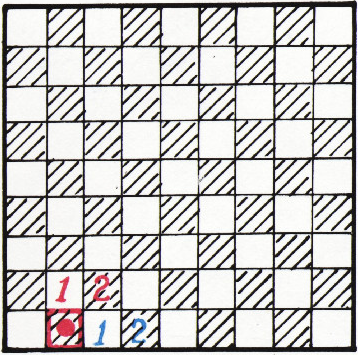
б) Если первоначально фишка стоит не на угловом поле, а на соседнем с ним, то выигрывает всегда начинающий. Для чётного $n$‍‍ это доказывается как выше (доска сразу разбивается на «доминошки», и первый игрок должен поступать как и раньше). Пусть $n$‍‍ нечётно. Тогда начинающий может «отрезать» угловое поле доски (второй игрок туда всё равно не попадёт, так как оно неподходящего цвета — см. рис. 2, в), после чего разбить оставшуюся часть доски на «доминошки» и снова поступать согласно описанной стратегии.

Предлагаем читателю разобраться в том, кто выигрывает, если первоначально фишка стоит на каком-то ином поле.