Условие задачи (1978, № 9) Задача М522 // Квант. — 1978. — № 9. — Стр. 36; 1979. — № 8. — Стр. 41.
На плоскости задано несколько непересекающихся отрезков, никакие два из которых не лежат на одной прямой. Мы хотим провести еще несколько отрезков, соединяющих концы данных отрезков так, чтобы все отрезки вместе образовали одну несамопересекающуюся ломаную. Всегда ли это можно сделать?
Изображения страниц
Решение задачи (1979, № 8) Задача М522 // Квант. — 1978. — № 9. — Стр. 36; 1979. — № 8. — Стр. 41.
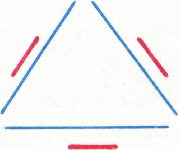
Ответ: не всегда. На рисунке 1 изображены шесть отрезков, концы которых нельзя соединить требуемым образом. В самом деле, каждый из шести концов коротких отрезков может быть соединён лишь с концом «своего» длинного отрезка, а поскольку свободных концов должно остаться два, то у одного из коротких отрезков оба его конца должны быть соединены отрезками с концами длинного. В результате получится замкнутая ломаная из четырёх звеньев — противоречие.

