Условие задачи (1978, № 4) Задача М500 // Квант. — 1978. — № 4. — Стр. 26—27; 1979. — № 2. — Стр. 34—35; 1979. — № 7. — Стр. 33—36.

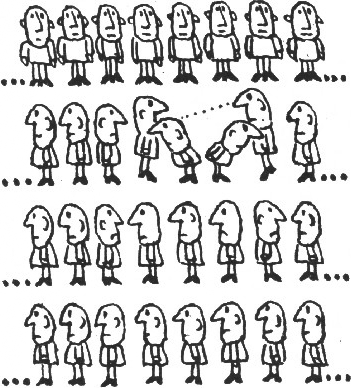
- Докажите, что через конечное время движение прекратится.
Какое наибольшее число раз мог повернуться «кругом» один человек?
Какое наибольшее количество времени могло продолжаться движение в строю?
- Пусть шеренга бесконечна в обе стороны, и по команде «нале-ВО» только конечное множество
$K$ первоклассников повернулось направо, а остальные — налево. Тогда по правилу задачи (выделенному курсивом) движение продолжалось бы бесконечно долго. Докажите, однако, что движение прекратится через конечное время, если это правило заменить таким: первоклассник поворачивается на$180^\circ$, только если первый (его сосед) и третий из стоящих перед ним обращены к нему лицом (рис. 2).
Изображения страниц
Решение задачи (1979, № 2) Задача М500 // Квант. — 1978. — № 4. — Стр. 26—27; 1979. — № 2. — Стр. 34—35; 1979. — № 7. — Стр. 33—36.
Мы решим задачи б) и в); задача а) следует из в) (или из б)).
б) Нетрудно видеть, что число поворотов, которые совершит первоклассник
в) Для времени движения справедлива та же оценка:


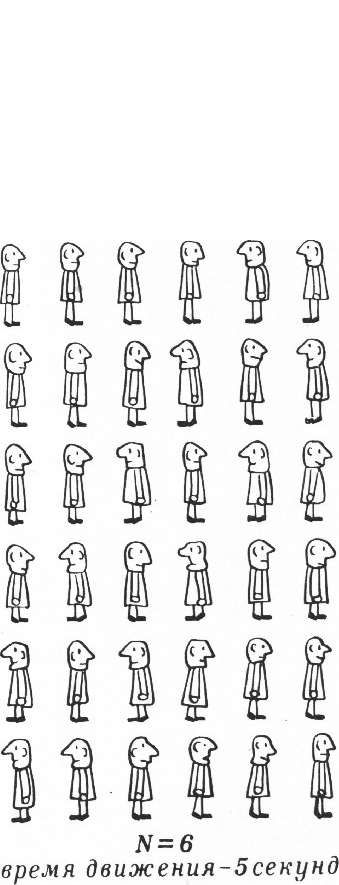
Будем теперь считать, что первоклассники, стоящие друг к другу лицом, не поворачиваются, а меняются местами (каждый из них делает шаг вперёд); картина от этого не изменится. Тогда нетрудно видеть (рис. 3), что:
- наличие последнего первоклассника никак не будет сказываться на движении предпоследнего;
- последний первоклассник может отстать от предпоследнего не более чем на два шага (между ними может стоять не более одного человека).
Из этого следует, что последний (смотрящий влево) первоклассник остановится не более чем через одну секунду после того, как окончательно прекратит движение предпоследний первоклассник (также смотрящий влево); а с остановкой последнего первоклассника движение в строю вообще прекращается (действительно, у него за спиной — только «правые», а перед ним — только «левые»). При этом движение в строю из
Решение задачи (1979, № 7) Задача М500 // Квант. — 1978. — № 4. — Стр. 26—27; 1979. — № 2. — Стр. 34—35; 1979. — № 7. — Стр. 33—36.
Решение задачи приведено в статье
Курдюмов Г. Консервативность бесконечного строя // Квант. — 1979. — № 7. — С. 33—36.







