Условие задачи (1976, № 9) Задача М403 // Квант. — 1976. — № 9. — Стр. 47; 1977. — № 6. — Стр. 46—47.
Докажите, что если в выпуклом многограннике из каждой вершины выходит чётное число рёбер, то в любом сечении его плоскостью, не проходящей ни через одну из его вершин, получится многоугольник с чётным числом сторон.
Изображения страниц
Решение задачи (1977, № 6) Задача М403 // Квант. — 1976. — № 9. — Стр. 47; 1977. — № 6. — Стр. 46—47.
Нетрудно убедиться, что наш многогранник можно раскрасить в два цвета — скажем белый и красный — так, чтобы любые две соседние (граничащие по ребру) грани имели разные цвета. В самом деле, расположим многогранник так, чтобы все его вершины находились на разной высоте (т. е. чтобы никакое ребро и никакая диагональ не были параллельны горизонтали — см. рис. 1). Проведём через самую верхнюю вершину горизонтальную плоскость. Постепенно опуская эту плоскость, мы раскрасим многогранник требуемым образом: поскольку в каждой вершине сходится чётное число граней, около верхней вершины мы можем выбрать цвет граней одним из двух возможных способов, а при прохождении каждой следующей вершины раскраска прилежащих к ней граней однозначно определяется.
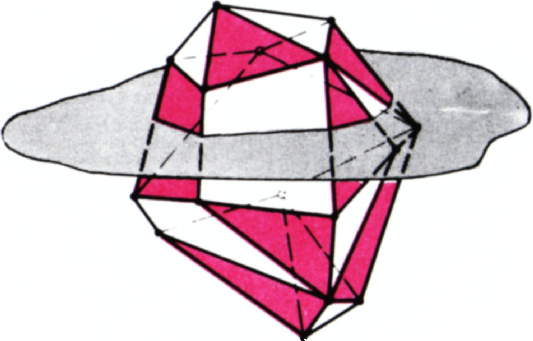
После того как многогранник раскрашен в два цвета, утверждение задачи становится очевидным: в каждом сечении, не проходящем через вершину, «белые» и «красные» стороны чередуются.


