Условие задачи (1974, № 5) Задача М264 // Квант. — 1974. — № 5. — Стр. 48—49; 1975. — № 1. — Стр. 46.
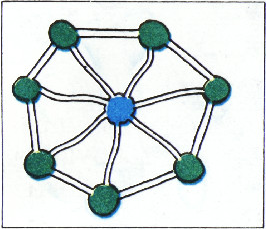
В городе одна синяя площадь и
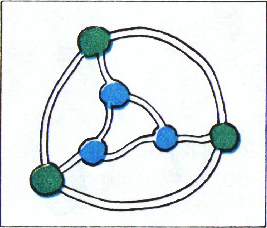
(Для города, план которого изображён на рисунке 4, аналогичное утверждение было бы неверным.)
Изображения страниц
Решение задачи (1975, № 1) Задача М264 // Квант. — 1974. — № 5. — Стр. 48—49; 1975. — № 1. — Стр. 46.
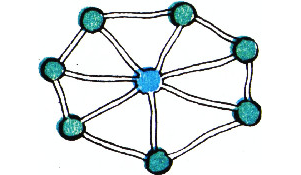
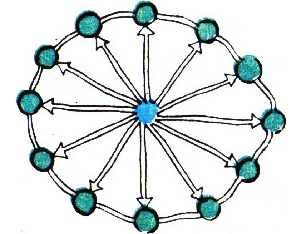
Прежде чем приступать к решению, отметим, что в условии задачи ссылка на рисунок 10 существенна — он является частью условия; так, например, для города, изображённого на рисунке 11 (с одной синей и
Перейдём теперь к решению нашей задачи. Разобьём доказательство на две части: докажем, что
а) от любой зелёной площади можно доехать до синей;
б) от синей площади можно доехать до любой зелёной.
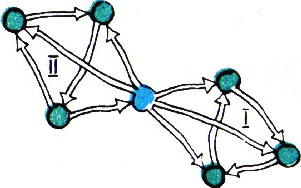
Условимся обозначать направление движения на улицах стрелочками.
а) Предположим, что от зелёной площади
б) Изменим направления всех стрелок. Полученная схема движения удовлетворяет условиям задачи. Поэтому, как показано в пункте а), при этой расстановке стрелок от любой зелёной площади можно доехать до синей. Но это и означает, что при старой расстановке стрелок от синей площади можно доехать до любой зелёной.
Обобщить задачу Б. Розенштейна о городе с односторонним движением можно так. Пусть в городе нет «тупиков» (в таком случае можно расставить направления на улицах так, что на каждую площадь можно приехать и с каждой уехать). Необходимое и достаточное условие того, что при любой такой расстановке стрелок от каждой площади можно доехать до любой другой, можно сформулировать так: любые два кольцевых маршрута (по городу, на улицах которого ещё не расставлены стрелки) должны проходить через одну площадь. Докажите это.


