Задача М191‍‍

Мы найдём последовательно множества (все они оказываются прямыми линиями, рис. 1): $m_1$‍‍ центров $O$‍;‍ $m_2$‍‍ середин отрезков $OA$‍‍ — точек $K$‍;‍ $m_3$‍‍ середин высот $OL$‍‍ равнобедренных треугольников $AOC$‍‍ — точек $P$‍;‍ $m_4$‍‍ середин отрезков $OC$‍‍ — точек $M$‍.‍

Множество $m_1$‍,‍ как хорошо известно, — прямая, проведённая перпендикулярно отрезку $AB$‍‍ через его середину. Обозначим через $D$‍‍ и $E$‍‍ точки пересечения прямой $m_1$‍‍ соответственно с прямой $l$‍‍ и с перпендикуляром, восставленным к прямой $l$‍‍ в точке $A$‍‍ (случай, когда прямые $m_1$‍‍ и $l$‍‍ параллельны, очень прост, но должен быть рассмотрен отдельно); через $G$‍‍ — середину отрезка $AE$‍;‍ через $F$‍‍ и $H$‍‍ — такие точки прямой $l$‍,‍ что $AF=FD=DH$‍‍ (рис. 1).

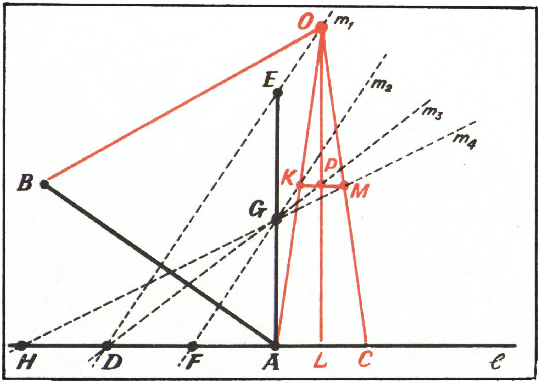
Теперь нужно доказать три утверждения:

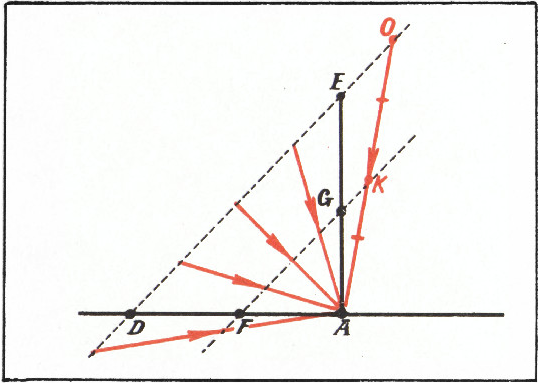
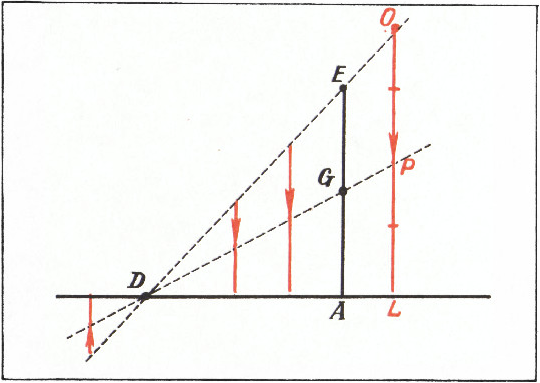
1. Множество середин отрезков, у которых один конец ($A$‍)‍ фиксирован, а другой расположен на данной прямой ($DE$‍),‍ — прямая линия ($FG$‍;‍ рис. 2).
2. Множество середин отрезков, параллельных заданному направлению ($AE$‍)‍ с концами на двух данных прямых ($ED$‍‍ и $AD$‍),‍ — прямая линия ($DG$‍;‍ рис. 3).
3. Множество вторых концов отрезков, параллельных заданному направлению ($l$‍),‍ первые концы и середины которых расположены на данных прямых ($FG$‍‍ и $DG$‍),‍ — прямая линия ($HG$‍;‍ рис. 4).

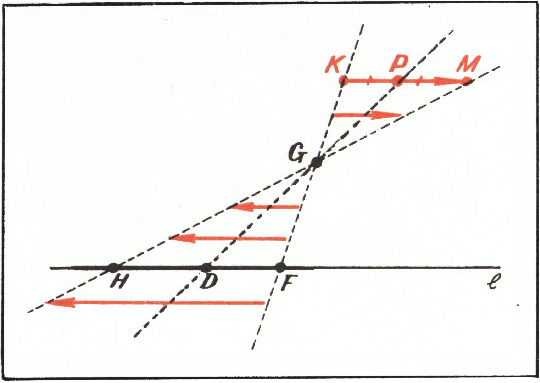
Все эти утверждения доказываются несложно и почти одинаково. Докажем для примера (3). Во‑первых, ясно, что любая точка $M$‍‍ на прямой $HG$‍‍ удовлетворяет нужному условию: если через точку $M$‍‍ провести прямую, параллельную $l$‍,‍ и обозначить через $K$‍‍ и $P$‍‍ её точки пересечения с прямыми $FG$‍‍ и $DG$‍,‍ то $P$‍‍ будет серединой отрезка $KM$‍‍ (это легко доказать с помощью подобия, используя равенство $HD=DF$‍).‍ Во‑вторых, на любой прямой, параллельной $l$‍,‍ очевидно, лежит только одна точка искомого множества. Поэтому других точек (не лежащих на прямой $HG$‍)‍ в этом множестве быть не может.

Остальные доказательства проведите сами.

Рассмотрите также случай, когда $AB\perp l$‍;‍ в этом случае все три прямые $(m_2)$‍,‍ $(m_3)$‍,‍ $(m_4)$‍‍ сливаются в одну, параллельную $l$‍‍ и делящую отрезок $AB$‍‍ в отношении $1:3$‍.‍