Задача М1502 / Задачи // Архив журнала «Квант»

Условие задачи (1995, № 4) Задача М1502 // Квант. — 1995. — № 4. — Стр. 24; 1996. — № 1. — Стр. 23.

Прямая отрезает от правильного $2n$‍‍-угольника со стороной 1 треугольник $APQ$‍‍ так, что $AP+AQ=1$‍‍ ($A$‍‍ — вершина $2n$‍‍-угольника). Найдите сумму углов, под которыми отрезок $PQ$‍‍ виден из всех вершин $2n$‍‍-угольника, кроме $A$‍.‍

В. В. Произволов

Открыть в номере

Изображения страниц

‍

Скачать PDF

Решение задачи (1996, № 1) Задача М1502 // Квант. — 1995. — № 4. — Стр. 24; 1996. — № 1. — Стр. 23.

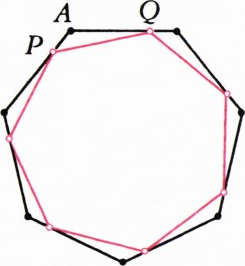
Вместо того чтобы менять положение вершины, из которой мы смотрим на отрезок $QP$‍,‍ можно вершину зафиксировать, а менять положение стороны (вращая $n$‍‍-угольник). Таким образом, интересующая нас сумма равна сумме углов, под которыми из точки $A$‍‍ видны все стороны правильного $n$‍‍-угольника, вписанного в данный, одна из сторон которого — $PQ$‍.‍ А эта сумма равна $\angle PAQ=\dfrac{\pi(n-2)}n$‍.‍

В. В. Произволов

Открыть в номере

Метаданные Задача М1502 // Квант. — 1995. — № 4. — Стр. 24; 1996. — № 1. — Стр. 23.

Предмет

Математика

Условие

Произволов В. В.

Решение

Произволов В. В.

Номера

1995. — № 4. — Стр. 24 [условие]

1996. — № 1. — Стр. 23 [решение]

Описание

Задача М1502 // Квант. — 1995. — № 4. — Стр. 24; 1996. — № 1. — Стр. 23.

Ссылка

https://www.kvant.digital/problems/m1502/