Задача М1489‍‍

Ответ: это всегда возможно для прямоугольников $m\times n$‍,‍ лишь если $m$‍‍ и $n$‍‍ не больше 3. Поскольку операции можно выполнять в обратном порядке, достаточно выяснить, для каких таблиц $m\times n$‍‍ из любой расстановки можно получить таблицу из одних единиц.

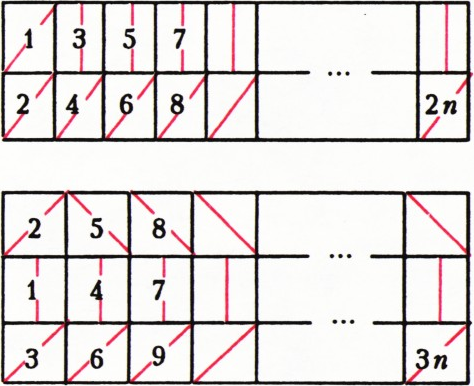
Легко видеть, что для прямоугольников $1\times n$‍,‍ $2\times n$‍‍ и $3\times n$‍‍ заменами знаков можно получить таблицу из одних единиц: на рисунке 1 указан порядок, в котором нули, стоящие в некоторых клетках, можно заменить на единицы (цветные линии показывают, какой именно — вертикальный или диагональный — «ход» следует делать).

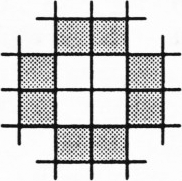
С другой стороны, в прямоугольнике $m\times n$‍,‍ где $m$‍‍ и $n$‍‍ не меньше 4, можно выделить фигуру из восьми клеток, показанных на рисунке 2 штриховкой; чётность количества единиц в этих клетках не меняется при всех разрешённых преобразованиях — является, как говорят, инвариантом. Таким образом, если в одной из таких фигур стоит нечётное число единиц, то прийти к таблице, заполненной единицами, невозможно.

Представляем читателям выяснить, образуют ли такие таблицы из 8 клеток полную систему инвариантов, т. е. следует ли из чётности количества единиц в каждой из них возможность преобразовать таблицу в состояние «все единицы», а заодно выяснить, сколько существует классов (неэквивалентных друг другу) таблиц относительно разрешённых в условии преобразований.