Задача М1471 / Задачи // Архив журнала «Квант»

Условие задачи (1995, № 1) Задача М1471 // Квант. — 1995. — № 1. — Стр. 23; 1995. — № 4. — Стр. 25—26.

Лыжник проехал через каждую из $n$‍‍ деревень по 2 раза и вернулся в исходную точку. Всегда ли по его лыжне можно проехать так, чтобы в каждой из этих $n$‍‍ деревень побывать ровно один раз (возвращаться в исходную точку не обязательно)?

М. Л. Гервер

Открыть в номере

Изображения страниц

‍

Скачать PDF

Решение задачи (1995, № 4) Задача М1471 // Квант. — 1995. — № 1. — Стр. 23; 1995. — № 4. — Стр. 25—26.

Ответ: нет, не всегда. Пример приведён на рисунке.

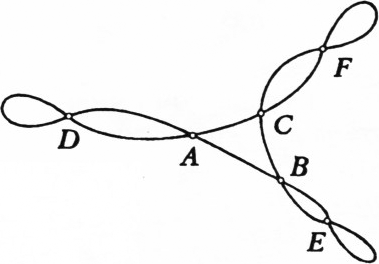
Предположим, что существует путь (по некоторым из линий на рисунке), проходящий через каждую из шести деревень только один раз. Из трёх деревень $D$‍,‍ $E$‍,‍ $F$‍‍ найдётся хотя бы одна, которая не является ни первой, ни последней на таком пути. Пусть это, скажем, деревня $D$‍.‍ Но тогда непосредственно перед ней и за ней путь проходит через $A$‍.‍ Противоречие.

Н. Б. Васильев, М. Л. Гервер

Открыть в номере

Метаданные Задача М1471 // Квант. — 1995. — № 1. — Стр. 23; 1995. — № 4. — Стр. 25—26.

Предмет

Математика

Условие

Гервер М. Л.

Решение

Васильев Н. Б.
, Гервер М. Л.

Номера

1995. — № 1. — Стр. 23 [условие]

1995. — № 4. — Стр. 25—26 [решение]

Описание

Задача М1471 // Квант. — 1995. — № 1. — Стр. 23; 1995. — № 4. — Стр. 25‍—‍26.

Ссылка

https://www.kvant.digital/problems/m1471/