Задача М130‍‍‍

Ответ: а) 4 точки; б) 8 точек. Примеры расположения такого количества точек: а) в вершинах квадрата; б) в вершинах куба.

(Разумеется, в условии подразумевается, что никакие три точки не должны лежать на одной прямой — без этого ограничения можно разместить сколько угодно точек.)

Докажем, что большее количество точек разместить нельзя.

Заметим прежде всего (это относится и к плоской, и к пространственной задаче), что если $A_i$‍‍ и $A_j$‍‍ — какие-то две из $n$‍‍ точек $A_1$‍,‍ $A_2$‍,‍ $\ldots$‍,‍ $A_n$‍,‍ удовлетворяющих условию задачи, то все эти точки должны принадлежать множеству таких точек $M$‍,‍ для которых одновременно $\angle MA_iA_j\le90^\circ$‍‍ и $\angle MA_jA_i\le90^\circ$‍.‍ Это множество — полоса между прямыми (в пространстве — плоскостями), проходящими через точки $A_i$‍‍ и $A_j$‍‍ и перпендикулярными к отрезку $A_iA_j$‍‍ (рис. 3); мы будем ниже обозначать эту полосу через $\mathit{\Pi}_{ij}$‍.‍

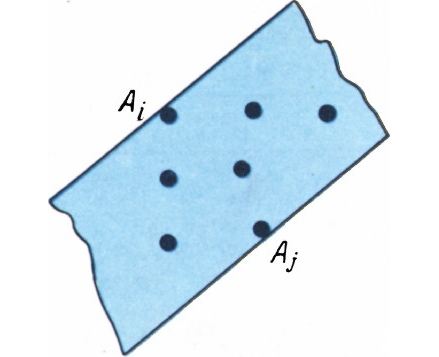
Из этого замечания следует, что если рассмотреть выпуклую оболочку $V$‍‍ данных $n$‍‍ точек — наименьший выпуклый многоугольник (многогранник), содержащий все эти точки, — то все точки $A_1$‍,‍ $A_2$‍,‍ $\ldots$‍,‍ $A_n$‍‍ должны лежать на границе множества $V$‍;‍ ни одна из них не может оказаться внутри $V$‍:‍ ведь $V$‍‍ содержится в каждой из полос $\mathit{\Pi}_{ij}$‍.‍

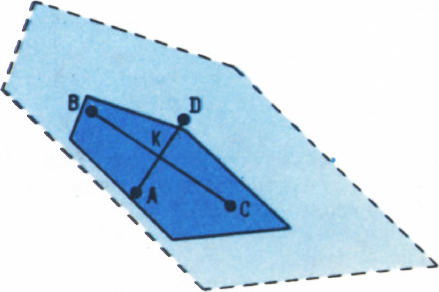
Решение задачи а) получается теперь в два слова. В этом случае $V$‍‍ — выпуклый $n$‍‍-угольник с вершинами $A_1$‍,‍ $A_2$‍,‍ $\ldots$‍,‍ $A_n$‍.‍ Сумма его углов равна $180^\circ(n-2)$‍,‍ и если каждый из углов не больше $90^\circ$‍,‍ то $180^\circ(n-2)\le90^\circ n$‍,‍ откуда $n\le4$‍.‍

Решение задачи на плоскости прислали многие читатели. Пространственная задача намного труднее, и полного доказательства мы не получили ни от кого из читателей. Приведём решение, которое впервые нашли известные геометры Л. Данцер и Б. Грюнбаум (1962 г.).

Рассмотрим кроме многогранника $V$‍‍ (здесь под $V$‍‍ можно понимать или выпуклую оболочку заданных $n$‍‍ точек $A_1$‍,‍ $A_2$‍,‍ $\ldots$‍,‍ $A_n$‍‍ или пересечение — общую часть — всех $\dfrac{n(n-1)}{2}$‍‍ полос $\mathit{\Pi}_{ij}$‍‍ ещё следующие многогранники: $V_i$‍,‍ получающиеся из $V$‍‍ сдвигом на вектор $\overrightarrow{A_1A_i}$‍‍ ($i=1$‍,‍ 2, $\ldots,$‍‍ $n$‍;‍ $V_1$‍,‍ разумеется, совпадает с $V$‍),‍ и $V'$‍,‍ получающийся из $V$‍‍ растяжением (гомотетией) с коэффициентом 2 и центром в точке $A_1$‍.‍ Докажем следующие три утверждения.

1. Многогранник, получающийся из $V$‍‍ сдвигом на вектор $\overrightarrow{A_iA_j}$‍,‍ не имеет общих внутренних точек с $V$‍‍ (т. е. может пересекаться с $V$‍‍ только на границе).
2. Никакие два из многогранников $A_1$‍,‍ $A_2$‍,‍ $\ldots$‍,‍ $A_n$‍‍ не имеют общих внутренних точек.
3. Все $V_i$‍‍ содержатся в $V'$‍.‍

Докажем 1°. При сдвиге на $\overrightarrow{A_iA_j}$‍‍ полоса $\mathit{\Pi}_{ij}$‍‍ переходит в новую полосу, которая не имеет с ней общих внутренних точек — эти две полосы имеют только общую граничную плоскость. Но $V$‍‍ содержится в $\mathit{\Pi}_{ij}$‍,‍ поэтому тем более верно 1°.

2° сразу следует из 1°: достаточно заметить, что $V_j$‍‍ получается из $V_i$‍‍ сдвигом на вектор $\overrightarrow{A_iA_j}$‍‍ (рис. 4).

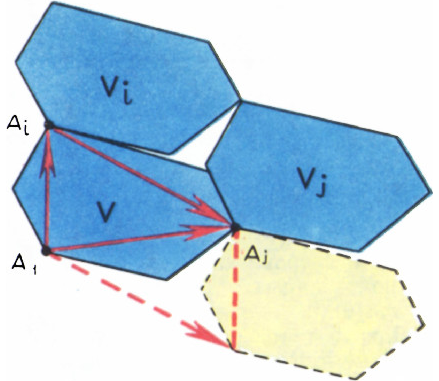
3° следует из более общего факта: если $ABC$‍‍ — три точки выпуклого многогранника $W$‍‍ и $W'$‍‍ — многогранник, полученный из $W$‍‍ растяжением в 2 раза с центром в точке $A$‍,‍ то четвёртая вершина $D$‍‍ параллелограмма $ABCD$‍‍ (т. е. точка, получающаяся из $C$‍‍ сдвигом на вектор $\overrightarrow{AB}$‍)‍ принадлежит $W'$‍.‍ Этот факт доказывается легко: точка $K$‍,‍ из которой при растяжении получается $D$‍‍ — середина отрезка $AD$‍‍ — является одновременно и серединой отрезка $BC$‍,‍ поэтому она принадлежит $W$‍‍ (ведь многогранник $W$‍‍ выпуклый), поэтому $D$‍‍ принадлежит $W'$‍‍ (рис. 5).

Итак, утверждения 2° и 3° доказаны. Пусть $v$‍‍ — объём многогранника $V$‍.‍ Тогда объём каждого из $V_i$‍‍ тоже равен $v$‍,‍ а объём $V'$‍‍ равен $8v$‍.‍ Из 2° и 3°, очевидно, следует, что $nv\le8v$‍,‍ откуда $n\le8$‍.‍

Заметим, что попутно мы решили задачу, предлагавшуюся на XIII Международной олимпиаде‍ (см. «Квант» № 12 за 1971 год, стр. 54, задача 2): видимо, задачу М130 б) в полном объёме международное жюри сочло слишком трудной для олимпиады и включило только вторую её половину.

В связи с доказанным утверждением возникает целый ряд вопросов, которые уже не удаётся решить тем красивым, но довольно искусственным способом, о котором мы рассказали. Например, какое наибольшее число точек в пространстве можно разместить так, чтобы все углы треугольников с вершинами в этих точках были острыми? Из нашего решения видно, что 8 точек расположить нельзя (убедитесь в этом). Нетрудно построить пример, когда точек 5. Может ли их быть 6? 7? Более общий и, вероятно, очень трудный вопрос — какое наибольшее число точек можно расположить так, чтобы все углы не превосходили данного $\alpha$‍?‍

Если кому-либо из читателей удастся продвинуться в решении этих вопросов, мы вернёмся к ним ещё раз.