Задача М1247‍‍

Ответ: а) можно; б) нельзя.

а) Пример покрытия (где квадрат со стороной 1 используется 4 раза, а остальные — по 3 раза) приведён на рисунке 1.

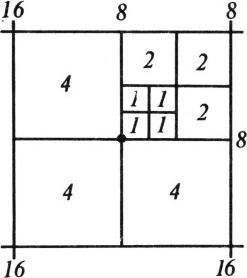
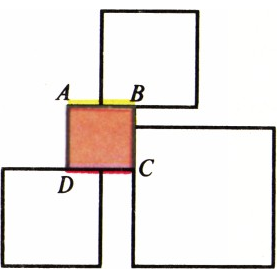
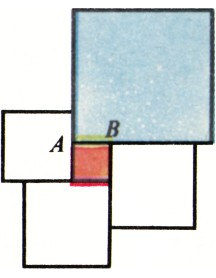
б) Предположим, что существует покрытие, в котором все квадраты различны. Поскольку сумма всех чисел, не превосходящих $2^{n-1}$‍,‍ меньше $2^n$‍‍ ($1+2+2^2+\ldots+2^{n-1}=2^n-1$‍),‍ то к каждой стороне любого из квадратов нашего покрытия должна примыкать сторона большего квадрата. Отсюда следует, что каждая вершина квадрата должна лежать на стороне большего квадрата (если вершина $B$‍‍ квадрата $ABCD$‍‍ лежит на стороне большего квадрата, примыкающего к стороне $AB$‍‍ (рис. 2), то вершина $C$‍‍ будет лежать на стороне большего квадрата, примыкающего к $BC$‍‍ и т. д.). Рассмотрим теперь наименьший из всех квадратов покрытия. Четыре квадрата будут примыкать к нему так, как показано на рисунке 3. Рассмотрим больший из этих квадратов — пусть он примыкает к стороне $AB$‍‍ наименьшего (на рисунке — это голубой квадрат). Тогда вершина $A$‍‍ этого квадрата не лежит на стороне большего, чем он, квадрата. Получили противоречие.