Задача М1123‍‍

Ответ на этот вопрос положителен. Одно из возможных расположений конструируется индукцией по степеням 2 (рис. 1). Пусть в квадрате $A_n$‍‍ размером $2^n\times2^n$‍‍ (на пересечении первых $2^n$‍‍ строк и $2^n$‍‍ столбцов) расположены числа от 1 до $2^n$‍‍ так, что каждое из них встречается по разу в каждой строке и каждом столбце. На рисунке 2 показано, как из $A_n$‍‍ изготавливается квадрат $A_{n+1}$‍‍ размером $2^{n+1}\times2^{n+1}$‍,‍ в котором расположены числа от 1 до $2^{n+1}$‍‍ и выполняется то же условие; запись $A_n+2^n$‍‍ здесь означает, что ко всем числам квадрата $A_n$‍‍ прибавляется $2^n$‍.‍

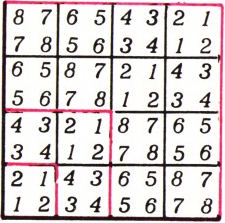
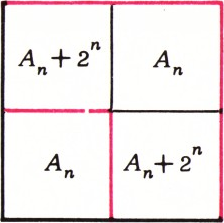
Эта задача связана с таким интересным вопросом. Пусть клетки бесконечной шахматной доски, занимающей прямой угол, занумерованы числами 0, 1, 2, $\ldots$‍‍ следующим образом: на первой угловой клетке ставится 0, а затем каждой клетке приписывается наименьший номер, не использованный ещё для нумерации каких-либо предшествующих клеток, стоящих левее неё на той же горизонтали или ниже неё — на той же вертикали. Какой номер получит клетка, стоящая на пересечении $i$‍‍-й горизонтали и $j$‍‍-й вертикали? (Номера приписываются клеткам в порядке возрастания суммы $i+j$‍;‍ см. задачу 127 в книге А. М. и И. М. Ягломов «Неэлементарные задачи в элементарном изложении», М.: Гостехтеориздат, 1954.)