Задача М1090‍‍

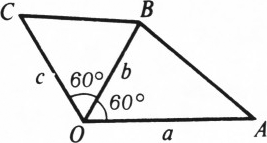
а) Доказываемое неравенство — это алгебраическая запись одного частного случая неравенства треугольника.

Отложим от произвольной точки $O$‍‍ три отрезка $OA=a$‍,‍ $OB=b$‍‍ и $OC=c$‍‍ так, что $\angle AOB=\angle BOC=60^\circ$‍,‍ $\angle AOC=120^\circ$‍‍ (см. рисунок). По теореме косинусов $$ AB=\sqrt{a^2+b^2-ab},\quad BC=\sqrt{b^2+c^2-bc},\quad AC=\sqrt{a^2+c^2-ac}, $$ a по неравенству треугольника $AB+BC\ge AC$‍.‍

б) Равенство возникает тогда и только тогда, когда точка $B$‍‍ попадает на отрезок $AC$‍‍ или, что равносильно, когда площадь треугольника $AOC$‍‍ равна сумме площадей $AOB$‍‍ и $BOC$‍,‍ т. е. $$ \dfrac12ac\sin120^\circ=\dfrac12(ab+bc)\sin60^\circ. $$ Деля обе части этого равенства на $\dfrac14abc\sqrt3$‍,‍ получим доказываемое условие $\dfrac1b=\dfrac1a+\dfrac1c$‍‍ $\left(\sin120^\circ=\sin60^\circ=\dfrac{\sqrt3}2\right)$‍.‍