Условие задачи (1988, № 1) Задача М1085 // Квант. — 1988. — № 1. — Стр. 21—22; 1988. — № 5. — Стр. 36—37.
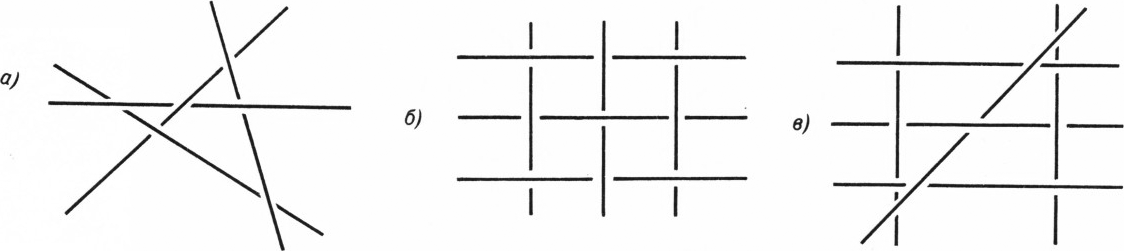
Несколько попарно скрещивающихся прямых, расположенных в пространстве, проектируются на горизонтальную плоскость. Их проекции изображены так, чтобы в точках пересечения было видно, какая точка расположена выше, а какая ниже. Может ли получиться проекция, изображённая на рисунке 1, а—в?
Изображения страниц
Решение задачи (1988, № 5) Задача М1085 // Квант. — 1988. — № 1. — Стр. 21—22; 1988. — № 5. — Стр. 36—37.
a) Ответ: нет. Допустим, что требуемое расположение (рис. 1, а) существует. Ясно, что прямую 1 можно опустить в вертикальной плоскости, не задевая прямую 3, так, чтобы она пересекла прямые 2 и 4, затем аналогично опустить прямую 3 так, чтобы она пересекла прямые 1 и 4 и, наконец, повернуть прямую 2 в вертикальной плоскости вокруг точки её пересечения с прямой 1 так, чтобы она пересекла прямую 3. При этом прямая 2 по-прежнему будет проходить под прямой 4 (рис. 2). Но в то же время прямые 2 и 4 должны пересекаться, так как каждая из них пересекает прямые 1 и 3, и следовательно, все четыре прямые должны лежать в одной плоскости. Противоречие.
б) Ответ: нет. Снова допустим, что рассматриваемая конфигурация возможна. Обозначим прямые через



