Изображения страниц
Текст статьи Савин А. П. Из куба — тетраэдр // Квант. — 1992. — № 3. — С. 11.
Участники международной конференции по синергетике, проходившей в 1990 году в Будапеште, уже успели утомиться от докладов. И тут на кафедру поднялся молодой японский учёный Ясуги Каякава. Зал оживился, когда он принялся вытаскивать из портфеля изящные конструкции, изготовленные из пластмассовых трубочек, которые в его руках начали трансформироваться в другие занятные формы.
Предлагаем одну из задач Каякавы, которую вполне можно считать новой головоломкой. Составьте из соломинок для коктейля и лески остов куба, пропуская леску через соломинки (рис. 1). (Мне для изготовления этой конструкции понадобилось всего три минуты.) А теперь попробуйте преобразовать полученную модель в остов тетраэдра, причём так, чтобы на каждом его ребре оказалось по две соломинки (рис. 2).
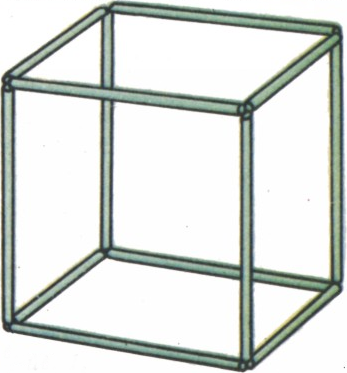

Я. Каякаве удалось доказать, что остов всякого полуправильного многогранника (что это такое, описано, например, в первом номере нашего журнала за 1978 г. в статье Матиясевич Ю. В. Модели многогранников) можно преобразовать либо в остов тетраэдра, либо в остов октаэдра. Попробуйте сами доказать, что остов октаэдра нельзя преобразовать в остов тетраэдра (хотя октаэдр, как и куб, имеет 12 рёбер).
