Асламазов Л. Г.

Что такое СКВИД?Асламазов Л. Г. Что такое СКВИД? // Квант. — 1981. — № 10. — С. 5‍—‍12.‍‍

О сверхпроводимости в наше время знают, наверное, все. Это явление состоит в том, что при низких температурах электрическое сопротивление ряда чистых металлов и сплавов становится равным нулю и электрический ток течёт без всяких потерь.

Температуры, при которых исчезает сопротивление, очень низкие — они близки к абсолютному нулю ($-273^\circ~\text{C}$‍).‍ Для охлаждения вещества до такой температуры его помещают в особую среду — жидкий гелий. При нормальном давлении гелий становится жидким при температуре 4,2 К и не замерзает при самых низких температурах — вплоть до абсолютного нуля.

Охлаждение до температур жидкого гелия — довольно сложная задача. Вот почему столь перспективное для использования в технике явление, как сверхпроводимость, пока ещё не нашло широкого практического применения. А, казалось бы, как заманчиво, например, передавать электрическую энергию на далёкие расстояния по сверхпроводящим проводам — никаких потерь! Однако охлаждать провода сейчас ещё довольно дорого. И хотя уже созданы сверхпроводящие линии передач длиной в несколько километров, а также сверхпроводящие моторы и генераторы и даже сверхскоростные поезда на так называемой магнитной подушке (где тоже используется сверхпроводимость) — такие установки в серийное производство всё ещё не запущены.

В лабораториях всего мира физики и химики ищут вещества, которые будут сверхпроводящими при не слишком низких температурах (например, чтобы для их охлаждения можно было использовать сравнительно дешёвый и доступный жидкий воздух). В этом направлении уже достигнут значительный прогресс — с каждым годом открывают всё более и более «высокотемпературные» сверхпроводники. Но даже сегодняшний рекордсмен — сплав ниобия с германием $\mathrm{Nb}_3\mathrm{Ge}$‍‍ — становится сверхпроводником лишь при температуре 22,4 К.

И тем не менее уже сейчас сверхпроводимость «работает». В ряде случаев возможности сверхпроводимости столь уникальны, что приходится мириться с затратами на OXлаждение. Так, сверхпроводящие магниты широко используются для создания сильных магнитных полей (в несколько десятков тесла); сверхпроводимость же применяют для измерения очень слабых магнитных полей (с точностью до $10^{-18}~\text{Тл}$‍).‍ На основе сверхпроводимости действуют чувствительнейшие вольтметры, детекторы и усилители электромагнитного излучения. Существует целая область электроники — криоэлектроника (от греческого слова «криос» — холод), основанная на использовании явления сверхпроводимости.

О некоторых практических применениях сверхпроводимости будет рассказано в этой статье. Однако рассказ придётся начать издалека. Давайте прежде познакомимся с одним красивым физическим явлением, лежащим в основе устройства многих сверхпроводящих приборов.

Квантование магнитного потока

Как известно, в микромире — мире молекул, атомов, элементарных частиц — существуют свои особые законы. Например, там многие физические величины могут принимать только определённые дискретные значения — как говорят физики, величины квантуются. (Для описания микромира создана специальная наука — квантовая механика.) В больших коллективах частиц — макроскопических телах — квантовые эффекты обычно перестают быть заметными, поскольку из-за хаотического теплового движения происходит усреднение величины по большому числу её различных значений и квантовые скачки «замазываются».

А что будет, если тело охладить до очень низких температур? Оказывается, в таком случае квантование может проявляться и в макроскопических масштабах. Пример тому даёт замечательное явление — квантование магнитного потока в сверхпроводнике.

Что такое магнитный поток $\mathit{\Phi}$‍,‍ знают все, кто изучал явление электромагнитной индукции: $$ \mathit{\Phi}=BS, $$ где $B$‍‍ — модуль вектора магнитной индукции, а $S$‍‍ — площадь поверхности, охватываемой контуром (для простоты будем считать, что индукция направлена по нормали к поверхности). Однако для многих будет открытием, что магнитный поток, создаваемый сверхпроводящим током, текущим, например, по кольцу, может принимать только определённые дискретные значения. Попробуем хотя бы упрощённо понять это явление.

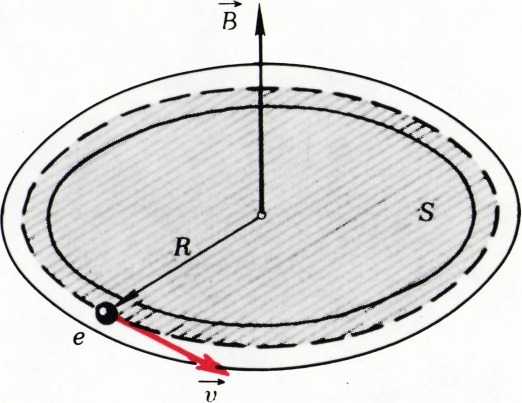
Движение сверхпроводящих электронов в кольце (рис. 1) похоже на движение электронов в атоме: электроны в кольце как бы движутся по гигантским орбитам радиуса $R$‍‍ без всяких столкновений. Поэтому естественно предположить, что их движение подчиняется тем же правилам квантования, что и движение электронов в атоме. Согласно постулату Бора, в атоме только определённые орбиты электронов являются стационарными, устойчивыми. Они отбираются с помощью следующего правила квантования: произведение модуля импульса электрона $mv$‍‍ на радиус орбиты $R$‍‍ (величина $mvR$‍‍ называется моментом импульса электрона) может принимать только дискретные значения, т. е. $$ mvR=n\hbar. $$ Здесь $n$‍‍ — целое положительное число, а величина $\hbar$‍,‍ определяющая наименьшее возможное изменение (квант) момента импульса, — постоянная Планка‍. Оказывается, квантование всех физических величин определяется именно этой универсальной постоянной. Она очень мала: $$ \hbar=1{,}05\cdot10^{-34}~\text{Дж}\cdot\text{с}, $$ поэтому квантовые эффекты проявляются, либо когда значения физических величин сами малы (в микромире), либо когда имеется много микрочастиц, движущихся совершенно одинаково. В последнем случае говорят о макроскопических квантовых явлениях, к которым и относится квантование магнитного потока в кольце со сверхпроводящим током.

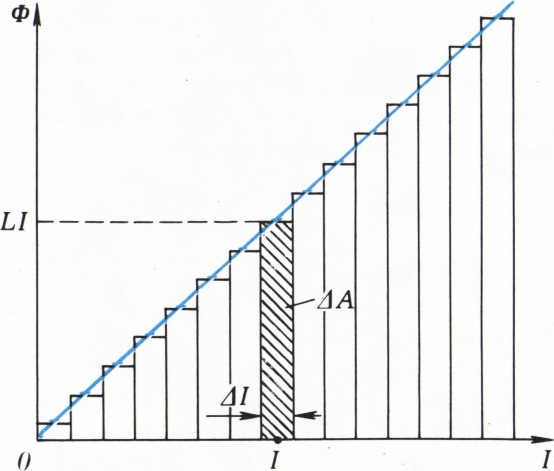
Найдём величину кванта магнитного потока. Магнитный поток $\mathit{\Phi}$‍‍ через кольцо связан с током $I$‍‍ соотношением $$ \mathit{\Phi}=LI, $$ где $L$‍‍ — индуктивность кольца. Ток $I$‍‍ можно выразить через скорость электронов $v$‍‍ и их число $N$‍.‍ Действительно, за время $t=\dfrac{2\pi R}v$‍‍ электроны совершают полный оборот; следовательно, за это время через любое поперечное сечение кольца пройдут все электроны, переносящие заряд $q=eN$‍‍ (где $e$‍‍ — заряд одного электрона). Поэтому ток в кольце $$ I=\dfrac qt=\dfrac{eNv}{2\pi R}. $$ Ещё одно соотношение, связывающее величины $v$‍,‍ $N$‍‍ и $I$‍,‍ можно получить, приравняв кинетическую энергию сверхпроводящих электронов к энергии кольца с током (см. «Приложение»): $$ N\dfrac{mv^2}2=\dfrac12LI^2. $$

Теперь выражение для магнитного потока можно представить в виде $$ \mathit{\Phi}=LI=\dfrac{LI^2}2\,\dfrac2I=N\dfrac{mv^2}2\,\dfrac{4\pi R}{eNv}= \dfrac{2\pi}emvR, $$ откуда следует, что магнитный поток пропорционален моменту импульса электронов. Но, согласно правилу квантования Бора, момент импульса может принимать только дискретные значения, поэтому и магнитный поток через кольцо, по которому течёт сверхпроводящий ток, тоже квантуется: $$ mvR=n\hbar\quad\text{и}\quad\mathit{\Phi}=\dfrac{2\pi}en\hbar. $$

Квант магнитного потока, который можно найти из предыдущей формулы, конечно, очень малая величина ($\sim10^{-15}~\text{Вб}$‍),‍ но тем не менее современные приборы позволяют наблюдать квантование магнитного потока. Такой опыт был проделан американскими учёными Дивером и Фейрбенком в 1961 году, только вместо кольца они использовали полую сверхпроводящую трубку, по которой циркулировали круговые сверхпроводящие токи. В опыте было обнаружено, что магнитный поток через площадь поперечного сечения трубки менялся действительно скачкообразно, однако величина кванта потока оказалась вдвое меньше приведённой выше. Объяснение этому даёт современная теория сверхпроводимости. Дело в том, что в сверхпроводящем состоянии электроны объединяются в пары и именно движением пар, имеющих заряд $2e$‍,‍ создаётся сверхпроводящий ток. Поэтому правильное значение $\mathit{\Phi}_0$‍‍ кванта магнитного потока получается, если в формулу квантования потока подставить удвоенный заряд электрона: $$ \mathit{\Phi}_0=\dfrac{2\pi\hbar}{2e}=2{,}07\cdot10^{-15}~\text{Вб}. $$

Вот так нашлась двойка, потерянная не только нами, но и английским учёным Лондоном, который теоретически предсказал квантование магнитного потока ещё в 1950 году — задолго до того, как была понята природа сверхпроводящего состояния.

Хочется подчеркнуть, что приведённый здесь вывод квантования магнитного потока, хотя и отражает правильно физическую сущность этого явления, слишком упрощённый. Даже удивительно, что таким образом можно получить правильное значение кванта магнитного потока. В действительности сверхпроводимость — сложное квантовое явление. Тем, кто хочет в нём разобраться по-настоящему, предстоит долгий путь от школьной физики до современной теории твёрдого тела — путь, на который потребуется много лет упорного, но увлекательного труда.

Эффект Джозефсона

Разберём ещё одно сверхпроводящее квантовое явление, которое послужило основой для создания целого ряда уникальных измерительных приборов. Речь пойдёт об эффекте Джозефсона, открытом сравнительно недавно — в 1962 году, но за который Джозефсону, английскому учёному, теоретически предсказавшему этот эффект, уже присуждена Нобелевская премия.

Представьте себе, что на стеклянную пластинку (как говорят, на подложку) нанесли плёнку сверхпроводника (обычно её получают, напыляя металл в вакууме). Затем её окислили, создав на поверхности слой диэлектрика (окисла) толщиной всего в несколько ангстрем‍. И снова покрыли плёнкой сверхпроводника. В результате получился так называемый сэндвич (в буквальном смысле этим английским словом называют два куска хлеба с сыром или другим чем-нибудь вкусным между ними). В сэндвичах и наблюдается эффект Джозефсона (для удобства измерений обычно сэндвич делают в виде креста, как показано на рисунке 2).

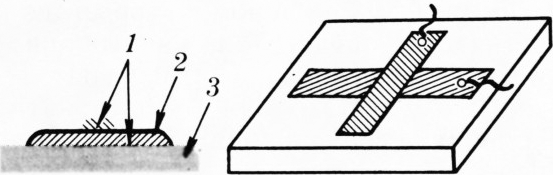
Давайте вначале обсудим случай, когда металлические плёнки находятся в нормальном (не сверхпроводящем) состоянии. Могут ли электроны из одной металлической плёнки (рис. 3, a) переходить в другую? Казалось бы, нет — им мешает слой диэлектрика. Для того чтобы выйти из металла, электрон должен обладать энергией, большей чем работа выхода, а при низких температурах электронов с такой энергией практически нет. На рисунке 3, б приведён график зависимости потенциальной энергии электрона $W$‍‍ от координаты $x$‍‍ (ось $X$‍‍ перпендикулярна к плоскости сэндвича). В металле электрон движется свободно, и его потенциальная энергия равна нулю. Для выхода в диэлектрик надо совершить работу выхода $W_{\text{в}}$‍,‍ которая больше, чем кинетическая, а значит и полная, энергия электрона $W_{\text{э}}$‍‍‍ Поэтому говорят, что электроны в металлических плёнках разделяет потенциальный барьер, высота которого равна $W_{\text{в}}-W_{\text{э}}$‍.‍

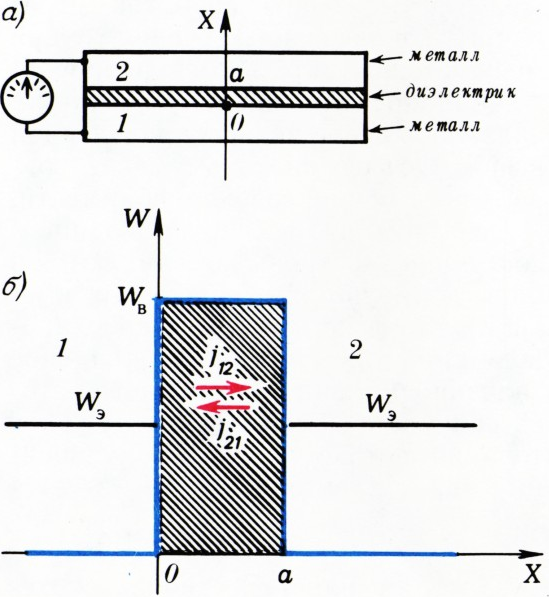
Если бы электроны подчинялись законам классической механики, то такой барьер для них был бы непреодолим. Но электроны — микрочастицы, а в микромире действуют особые законы, которые позволяют многое, недоступное большим телам. Человеку, например, с такой энергией на горку не взобраться, а вот электрон может пройти сквозь неё! Он как бы роет под горкой туннель и проникает, даже если его энергии не хватает, чтобы взобраться на горку. Конечно, не следует всё это понимать буквально. Туннельный эффект (так называют это явление) объясняется волновыми свойствами микрочастиц, и по-настоящему в нём можно разобраться, только изучив квантовую механику. Но факт остаётся фактом: с некоторой вероятностью электроны могут проникать через диэлектрик из одной металлической плёнки в другую. Эта вероятность тем больше, чем меньше высота $W_{\text{в}}-W_{\text{э}}$‍‍ барьера и чем меньше его ширина $a$‍.‍

Итак, тонкая плёнка диэлектрика оказывается проницаемой для электронов — через неё может течь так называемый туннельный ток. Однако суммарный туннельный ток равен нулю: сколько электронов переходит из нижней металлической плёнки в верхнюю, столько же в среднем переходит, наоборот, из верхней плёнки в нижнюю.

Как же сделать туннельный ток отличным от нуля? Для этого надо нарушить симметрию, например — присоединить металлические плёнки к источнику тока с напряжением $U$‍‍ (рис. 4, а). Тогда плёнки будут играть роль обкладок конденсатора, а в слое диэлектрика возникнет электрическое поле с напряжённостью $E=\dfrac Ua$‍.‍ Работа по перемещению заряда $e$‍‍ на расстояние $x$‍‍ вдоль направления поля равна $A=Fx=eEx=\dfrac{eUx}a$‍,‍ и поэтому график потенциальной энергии электрона приобретает вид, показанный на рисунке 4, б. Как видно, электронам из верхней плёнки ($x\gt a$‍)‍ преодолеть барьер легче, чем электронам из нижней плёнки ($x\lt0$‍),‍ которым надо подскочить на более высокий уровень. В результате даже при малых напряжениях источника возникнет туннельный ток.

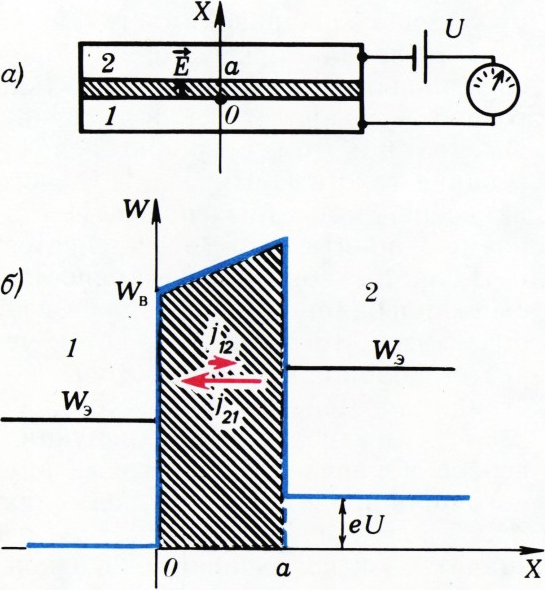
Туннельные контакты из нормальных металлов используются в некоторых приборах, но в этой статье речь идёт о практическом применении сверхпроводимости. Поэтому сделаем следующий шаг и представим себе, что металлические плёнки, разделённые тонким слоем диэлектрика, находятся в сверхпроводящем состоянии. Как будет вести себя туннельный сверхпроводящий контакт? Оказывается, сверхпроводимость приводит к совсем неожиданным результатам.

Как уже говорилось, электроны из верхней плёнки имеют избыточную энергию $eU$‍‍ по сравнению с электронами нижней плёнки. Эту энергию они приобретают, ускоряясь электрическим полем в слое диэлектрика, через который туннелируют. Оказавшись в нижней плёнке, они должны сбросить лишнюю энергию и перейти в равновесное состояние. Если бы плёнка находилась в нормальном состоянии, то осуществить это было бы легко — достаточно нескольких столкновений с кристаллической решёткой металла и лишняя энергия электронов в конечном счёте переходит в тепло. Но плёнка находится в сверхпроводящем состоянии, и передать энергию решётке электроны не в состоянии! Вот и остаётся только электронам излучить эту энергию в виде кванта электромагнитного излучения с энергией $h\omega$‍.‍ Поэтому частота излучения о связана с приложенным напряжением $U$‍‍ простым соотношением $$ h\omega=2eU. $$ Вы заметили, что справа написан удвоенный заряд электрона — надо помнить, что туннелируют не отдельные электроны, а сверхпроводящие пары.

Вот какой удивительный эффект был предсказан Джозефсоном: постоянное напряжение, приложенное к сверхпроводящему туннельному контакту (его называют также джозефсоновским элементом), приводит к генерации электромагнитного излучения. Экспериментально этот эффект впервые был обнаружен в Харьковском физико-техническом институте низких температур учёными И. М. Дмитриенко, В. М. Свистуновым и И. К. Янсоном в 1965 году.

Первое, что приходит в голову, если говорить о практическом использовании эффекта Джозефсона, — это создание генератора электромагнитного излучения. Но в действительности всё не так просто: излучение довольно трудно вывести из узкой щели между сверхпроводящими плёнками, где оно генерируется (именно поэтому экспериментальное обнаружение эффекта Джозефсона было непростой задачей), да и мощность излучения очень мала. Поэтому сейчас джозефсоновские элементы используются в основном в качестве детекторов электромагнитного излучения, но зато самых чувствительных в некоторых диапазонах частот.

Такое применение основано на явлении резонанса между внешними электромагнитными колебаниями (в регистрируемой волне) и собственными колебаниями, возникающими в джозефсоновском элементе при приложении к нему постоянного напряжения. Собственно говоря, резонанс лежит в основе работы многих приёмников: волну удаётся «поймать», когда её частота совпадает с частотой приёмного колебательного контура. В качестве приёмного контура удобно использовать джозефсоновский элемент: частоту его собственных колебаний легко подстраивать (изменяя напряжение), а острота резонанса, определяющая чувствительность приёмника, оказывается очень высокой. По такому принципу уже созданы самые чувствительные приёмники электромагнитного излучения, которые используются для исследования излучения Вселенной.

Квантовый магнитометр

Эффект Джозефсона в сочетании с явлением квантования магнитного потока послужили основой для создания целого семейства сверхчувствительных измерительных приборов. Они называются «сверхпроводящие квантовые интерференционные приборы» или «СКВИДы» (по сочетанию первых букв соответствующих английских слов Superconducting Quantum Interference Devісеѕ‍. Об одном из них — квантовом магнитометре (приборе для измерения слабых магнитных полей) — будет рассказано в этой главе.

Простейший квантовый магнитометр состоит из сверхпроводящего кольца, в цепь которого включён джозефсоновский элемент (рис. 5). Как вы уже знаете, для того чтобы возник ток в нормальном туннельном контакте, к нему надо приложить хотя бы небольшое напряжение. А вот в сверхпроводящем туннельном контакте это не обязательно. Если в кольце создать сверхпроводящий ток, то он сможет течь и через джозефсоновский элемент: сверхпроводящие пары будут туннелировать через тонкий слой диэлектрика. Такое явление называют стационарным (постоянным во времени) эффектом Джозефсона, в отличие от нестационарного эффекта, сопровождаемого излучением (о нём было рассказано в предыдущей главе). Существует, однако, максимально допустимое для контакта значение сверхпроводящего тока (его называют критическим током контакта $I_{\text{к}}$‍.‍ При токе, большем критического, сверхпроводимость в контакте разрушается и на нем обязательно появляется напряжение (эффект Джозефсона становится нестационарным).

Итак, при включении в сверхироводящий контур джозефсоновского элемента не происходит полного разрушения сверхпроводимости, но в контуре появляется место, в котором сверхпроводимость ослаблена (как говорят, возникает слабая связь). Именно на этом основано использование такого контура для точного измерения магнитных полей. Постараемся понять, как это делается.

Если бы контур был полностью сверхпроводящим (не содержал слабой связи), то магнитный поток через его площадь был бы строго постоянным. Действительно, согласно закону электромагнитной индукции, всякое изменение внешнего магнитного поля приводит к возникновению ЭДС индукции $\mathscr{E}_i=-\dfrac{\Delta\mathit{\Phi}_{\text{внеш}}}{\Delta t}$‍,‍ a значит — к изменению тока в контуре. Но изменяющийся ток в свою очередь порождает ЭДС самоиндукции $\mathscr{E}_{is}=-L\dfrac{\Delta I}{\Delta t}$‍.‍ Поскольку падение напряжения в сверхпроводящем контуре равно нулю (сопротивление равно нулю), алгебраическая сумма этих ЭДС тоже равна нулю: $$ \mathscr{E}_i+\mathscr{E}_{is}=0, $$ или $$ \dfrac{\Delta\mathit{\Phi}_{\text{внеш}}}{\Delta t}+ L\dfrac{\Delta I}{\Delta t}=0. $$ Отсюда следует, что при изменении внешнего магнитного потока сверхпроводящий ток в контуре меняется так, чтобы изменение магнитного потока, создаваемого током, компенсировало изменение внешнего потока (правило Ленца). При этом полный магнитный поток через контур остаётся постоянным: $\mathit{\Phi}=\text{const}$‍.‍ Изменить его, не переводя контур в нормальное состояние, нельзя (говорят, что в сверхпроводящем контуре магнитный поток «заморожен»).

А что произойдёт, если сверхпроводящий контур содержит слабую связь? Оказывается, что магнитный поток через такой контур может меняться — через слабую связь в контур проникают кванты потока (как вы уже знаете, магнитный поток сверхпроводящего тока квантуется — он равен целому числу квантов потока $\mathit{\Phi}_0$‍).‍

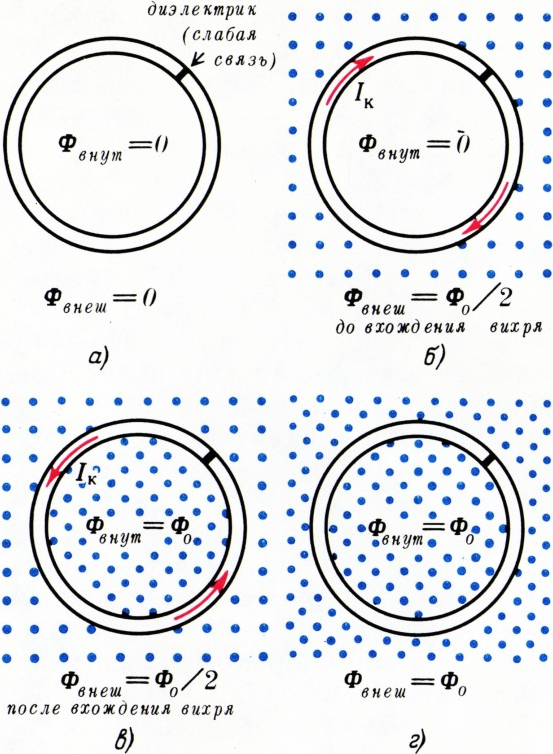
Давайте проследим, как меняются магнитный поток внутри сверхпроводящего кольца со слабой связью и величина тока в кольце при изменении внешнего магнитного поля. Пусть вначале внешнее поле и ток в контуре равны нулю (рис. 5, а). Тогда поток внутри контура тоже равен нулю. Будем увеличивать внешнее поле — в контуре появится сверхпроводящий ток, магнитный поток которого в точности компенсирует внешний поток. Так будет продолжаться до тех пор, пока ток в контуре не достигнет критического значения $I_{\text{к}}$‍‍ (рис. 5, б). Предположим для определённости, что в этот момент внешнее поле создаёт поток, равный половине кванта: $\dfrac12\mathit{\Phi}$‍‍‍.

Как только ток станет равным $І_{\text{к}}$‍,‍ сверхпроводимость в месте слабой связи разрушится, и в контур войдёт квант потока $\mathit{\Phi}_0$‍,‍ (рис. 5, в). При этом отношение $\dfrac{\mathit{\Phi}_{\text{внут}}}{\mathit{\Phi}_0}$‍‍ скачком увеличится на единицу (как говорят, сверхпроводящий контур перейдёт в новое квантовое состояние). А что произойдёт с током? Его величина останется прежней, но направление изменится на противоположное. Действительно, если до вхождения кванта потока $\mathit{\Phi}_0$‍,‍ ток $I_{\text{к}}$‍‍ полностью экранировал внешний поток $\dfrac12\mathit{\Phi}_0$‍,‍ то после вхождения он должен усиливать внешний поток $\dfrac12\mathit{\Phi}_0$‍‍ до значения $\mathit{\Phi}_0$‍.‍ Поэтому в момент вхождения кванта потока направление тока скачком меняется на противоположное.

При дальнейшем увеличении внешнего поля ток в кольце начнёт уменьшаться, сверхпроводимость в кольце восстановится и поток внутри кольца будет оставаться равным $\mathit{\Phi}_0$‍.‍ Ток в контуре обратится в нуль, когда внешний поток также станет равным $\mathit{\Phi}_0$‍‍ (рис. 5, г), а затем он начнёт течь в обратном направлении (опять экранировка!). Наконец, при значении внешнего потока $\dfrac32\mathit{\Phi}_0$‍‍ ток опять станет равным $I_{\text{к}}$‍,‍ сверхпроводимость разрушится, войдёт следующий квант потока и т. д.

Графики зависимости магнитного потока $\mathit{\Phi}_{\text{внут}}$‍‍ внутри кольца и тока $I$‍‍ в нём от величин внешнего потока $\mathit{\Phi}_{\text{внеш}}$‍‍ показаны на рисунке 6 (оба потока измеряются в естественных единицах — квантах потока $\mathit{\Phi}_0$‍).‍ Ступенчатый характер зависимости позволяет «чувствовать» отдельные кванты потока, хотя величина их очень мала (порядка $10^{-15}~\text{Вб}$‍).‍ Нетрудно понять почему. Магнитный поток внутри сверхпроводящего контура изменяется хотя и на малую величину $\Delta\mathit{\Phi}=\mathit{\Phi}_0$‍,‍ но скачком, т. е. за очень короткий промежуток времени $\Delta t$‍.‍ Так что скорость изменения магнитного потока $\dfrac{\Delta\mathit{\Phi}}{\Delta t}$‍‍ при таком скачкообразном характере изменения потока оказывается очень большой. Её можно измерить, например, по величине ЭДС индукции, наводимой в специальной измерительной катушке прибора. В этом и состоит принцип работы квантового магнитометра.

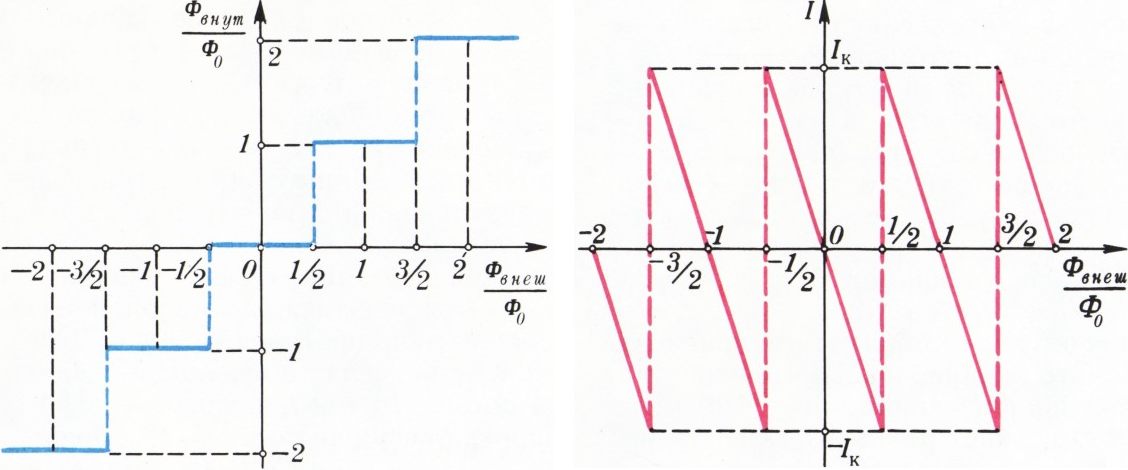
Устройство реального квантового магнитометра в действительности много сложнее. Так, обычно используют не одну, а несколько слабых связей, включённых параллельно, — своеобразная интерференция сверхпроводящих токов приводит к повышению точности измерений (поэтому такие приборы и называются интерференционными). Чувствительный элемент прибора индуктивно связывают с катушкой колебательного контура, где скачки потока преобразуются в импульсы напряжения, которые затем усиливаются. Но рассказ обо всех этих тонкостях выходит за рамки данной статьи.

Заметим, что в наши дни сверхчувствительные магнитометры, измеряющие магнитные поля с точностью до $10^{-15}~\text{Тл}$‍,‍ — это уже промышленная продукция, находящая широкое применение в измерительной технике. Недалёк, например, тот день, когда магнитокардиограммы‍, снимаемые с помощью СКВИДов, принципиально изменят существующие возможности для диагностики сердечных заболеваний.

Приложение

Формулу для энергии кольца с током можно получить, например, так. Представим себе, что сверхпроводящее кольцо подключается к источнику тока с ЭДС $\mathscr{E}$‍.‍ В кольце появится ток, который будет всё время нарастать. При этом скорость изменения тока $\dfrac{\Delta I}{\Delta t}$‍‍ должна быть такой, чтобы ЭДС самоиндукции $\mathscr{E}_{is}=-L\dfrac{\Delta I}{\Delta t}$‍‍ компенсировала внешнюю ЭДС $\mathscr{E}$‍‍ (сопротивление сверхпроводника, а следовательно, и падение напряжения на нём равны нулю): $$ \mathscr{E}_{is}=-\mathscr{E}. $$ При прохождении по цепи заряда $\Delta Q=I\,\Delta t$‍‍ источник совершает работу $$ \Delta A=\mathscr{E}\,\Delta Q=L\,\dfrac{\Delta I}{\Delta t}\,I\,\Delta t= LI\,\Delta I. $$ Произведение $LI$‍‍ — это магнитный поток $\mathit{\Phi}$‍‍ через площадь кольца. Для того чтобы нагляднее представить полученный результат, нарисуем график зависимости $\mathit{\Phi}$‍‍ от $I$‍‍ (рис. 7). Как видно из рисунка, элементарная работа $\Delta A$‍‍ равна площади заштрихованного прямоугольника. Полная работа $A$‍‍ при изменении тока от 0 до $I_0$‍‍ равна сумме площадей прямоугольников с высотами, равными соответствующим значениям магнитного потока, т. е. площади треугольника со сторонами $I_0$‍‍ и $LI_0$‍:‍ $$ A=\dfrac12(LI_0)I_0=\dfrac12LI_0^2. $$ Эта работа как раз и равна энергии тока в кольце. Разумеется, полученное выражение не зависит от того, какой ток течёт в кольце — сверхпроводящий или нормальный.