Изображения страниц
Текст статьи Задачи наших читателей // Квант. — 1980. — № 8. — С. 11.
Докажите, что для
$0\le a\le b$ выполняется неравенство $$ \ln\dfrac ba\le\dfrac{b^2-a^2}{2ab}. $$Докажите, что если некоторый член последовательности 1, 31, 331, 3331,
$\ldots$ делится на 541, то он также делится и на 19.Докажите, что если $$ x=a_1+\dfrac1{a_2+\dfrac1{a_3+\displaystyle{\mathstrut\atop\!{\ddots}+\dfrac1{a_{n-1}+\dfrac1{a_n-y}}}}}, $$ то $$ y=a_n+\dfrac1{a_{n-1}+\dfrac1{a_{n-2}+\displaystyle{\mathstrut\atop\!{\ddots}+\dfrac1{a_2+\dfrac1{a_1-x}}}}}. $$
-
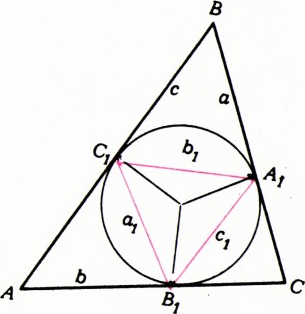
Пусть
$a$, $b$, $c$ — длины сторон треугольника$ABC$, $a_1$, $b_1$, $c_1$ — соответствующие длины сторон треугольника$A_1B_1C_1$ с вершинами в точках касания виисанной в тpeугольник$ABC$ окружности (см. рисунок). Докажите, что $$ \dfrac{a^2}{a_1^2}+\dfrac{b^2}{b_1^2}+\dfrac{c^2}{c_1^2}\ge12. $$ На основании прямого кругового конуса построен цилиндр. Докажите, что при пересечении этого цилиндра плоскостью, касающейся конуса, получается эллипс, площадь которого равна боковой поверхности конуса.
В равнобедренном треугольнике биссектриса угла при основании вдвое длиннее биссектрисы угла при вершине. Найдите углы этого треугольника.
Докажите, что центр вписанной в треугольник
$ABC$ окружности, точка пересечения его медиан и точка пересечения отрезков, соединяющих вершины треугольника$ABC$ с точками касания его сторон с вневписанными окружностями (вневписанная окружность — это окружность, касающаяся стороны треугольника и продолжений двух других его сторон), находятся на одной прямой.Докажите, что во всяком треугольнике $$ m_a^2=\left(\dfrac{b+c}2\right)^2-bc\sin^2\dfrac{\widehat A}2, $$ где
$m_a$ — длина медианы, проведённой к стороне, лежащей против угла$A$, $b$ и$c$ — длины двух других сторон треугольника,$\widehat A$ — величина угла$A$. Множество
$M$ содержит конечное число$n\gt2$ точек плоскости, которые не лежат на одной прямой, причём, если некоторые три точки этого множества образуют треугольник, то точка пересечения высот этого треугольника также принадлежит множеству$M$. Какие значения может принимать$n$? Функцию
$F$, определённую на множестве всех целых чисел и принимающую неотрицательные целые значения, мы будем называть современной, если для любых целых$m$, $n$ выполняются соотношения $$ F(mn)=F(m)\,F(n),\quad F(m+n)\le1980[F(m)+F(n)] $$ и, кроме того,$F(1980)=0$. Найдите все современные функции.
Найдите наибольшее число способов, которыми один треугольник можно вписать в другой (вершины вписанного треугольника находятся на различных сторонах описанного).
Без помощи таблиц докажите неравенства
- $$\cos42^\circ\lt\dfrac34;$$
- $$\tg70^\circ\gt\dfrac{19}7.$$
В выражениях вида
$\sqrt{A\pm\sqrt B}$ часто можно избавиться от двойного корня, воспользовавшись формулой $$ \sqrt{1\pm2\cos\alpha\sin\alpha}=\lvert\cos\alpha\pm\sin\alpha\rvert. $$ Например: $$ \sqrt{13\pm\sqrt{48}}=\sqrt{13}\sqrt{1\pm2\sqrt{\dfrac{12}{13}} \sqrt{\dfrac1{13}}}=\sqrt{13}\left(\dfrac{\sqrt{12}}{\sqrt{13}}\pm \dfrac1{\sqrt{13}}\right)=\sqrt{12}\pm1. $$ Вот несколько примеров для самостоятельного решения:$\sqrt{2\pm\sqrt3}$; $\sqrt{11\pm\sqrt{21}}$; $\sqrt{9\pm4\sqrt2}$.
Ответы, указания, решения
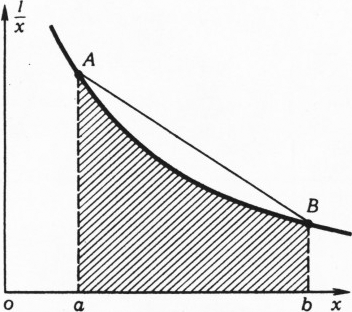
- Поскольку функция
$x\to\dfrac1x$ при$x\gt0$ выпукла вниз, площадь трапеции$aABb$ (см. рисунок) больше площади заштрихованной трапеции, т. е. $$ \dfrac12\left(\dfrac1b+\dfrac1a\right)(b-a)\ge\int\limits_a^b\dfrac{dx}x= \ln x\,\Big|_a^b=\ln\dfrac ba. $$ Общий член последовательности 1, 31, 331,
$\ldots$ имеет вид$a_n=\dfrac{10^n-7}3$. Просмотрев остатки от деления чисел$10^n$ на 19($n=1$, 2, 3,$\ldots$, 18; дальше остатки повторяются), легко доказать, что$a_n$ делится на 19 тогда и только тогда, когда$n=18m+12$. Аналогично можно доказать, что$a_n$ делится на 541 тогда и только тогда, когда$n=540k+534$. Если
$a_n$ делится на 541, то $$ n=540k+534=18(30k+29)+12, $$ и значит,$a_n$ делится на 19.- Из условия имеем $$ \def\dd#1{\displaystyle{\mathstrut\atop\!{\ddots}+#1}} \begin{gather*} a_1-x=\dfrac1{-a_2-\dfrac1{a_3+\dd{\dfrac1{a_n-y}}}},\\ \Downarrow\\ \dfrac1{a_1-x}=-a_2-\dfrac1{a_3+\dd{\dfrac1{a_n-y}}},\\ \Downarrow\\ a_2+\dfrac1{a_1-x}=\dfrac1{-a_3-\dfrac1{a_4+\dd{\dfrac1{a_n-y}}}},\\ \Downarrow\\ \dfrac1{a_2+\dfrac1{a_1-x}}=-a_3-\dfrac1{a_4+\dd{\dfrac1{a_n-y}}},\\ \Downarrow\\ {\ldots}\,{\ldots}\,{\ldots}\\ \Downarrow\\ a_{n-1}+\dfrac1{a_{n-2}+\dd{\dfrac1{a_3+\dfrac1{a_2+\dfrac1{a_1-x}}}}}= \dfrac1{-a_n+y}, \end{gather*} $$ откуда получаем результат.
- Отразим
$\triangle ABC$ относительно основания$AC$, получим ромб$ABCB_1$. Поскольку$[AB_1]\parallel[BC]$ и$|AE|=|BB_1|$, четырёхугольник$ABEB_1$ — равнобедренная трапеция. Отсюда следует, что$\widehat{B_1BE}=\widehat{AEB}=\alpha$. Обозначим$\widehat{BAE}$ через$\beta$. Тогда из треугольников$ABC$ и$ABE$ получаем: $$ \left\{\begin{array}{l} 2\beta+2\alpha+2\beta=180^\circ,\\ \beta+2\alpha+\alpha=180^\circ, \end{array}\right. $$ т. е.$\alpha=3\beta$. Подставляя это значение$\alpha$ в первое уравнение, находим$\beta=18^\circ$, $\alpha=54^\circ$.

