Изображения страниц
Текст статьи Савин А. П. Кое-что о выпуклости // Квант. — 1979. — № 1. — С. 42—44.
Изучая геометрию в школе, вы встречаетесь с разными плоскими и пространственными фигурами. Так, вы уже знаете, что такое треугольник, квадрат, окружность, куб, пирамида, шар, конус, цилиндр. Конечно, этот перечень далеко не исчерпывает всего разнообразия форм, существующих в природе. Огромное количество замысловатых и причудливых форм способно создать и человеческое воображение. Естественно, что лишь немногие из этих форм имеют названия. Да и нужно ли все их назвать?
Когда садовод сокрушается: «Проклятые птицы склевали у меня все вишни!» — ему безразлично, какие именно птицы это сделали — воробьи, дрозды или попугаи. Он говорит о существах, которые летают, садятся на ветки деревьев и не прочь полакомиться сочными вишнями. Знаете ли вы, что существует 8616 различных видов птиц? Можно ли запомнить все их названия? Конечно, нет. Зоологи разделили всех птиц на 40 отрядов: голуби, чайки, воробьиные и т. д., объединив в один отряд птиц, обладающих похожими свойствами. И если вы будете знать эти сорок отрядов, а также два-три десятка названий птиц, обитающих в вашей местности, то знакомство с птицами можно уже считать состоявшимся.
Так и в геометрии: вы знакомитесь с наиболее часто встречающимися фигурами. А можно ли выделить какие-нибудь интересные совокупности — «отряды» фигур? Да, и это одна из целей геометрии. Свойство, которое объединяет фигуры в тот «отряд», о котором мы хотим рассказать, называется выпуклостью.
Слово выпуклый не является для вас новым. Однако попробуйте дать этому понятию чёткое определение и вы увидите, что это сделать не так уж просто. Посмотрим, как это понятие определяется в «Словаре русского языка» С. И. Ожегова. Читаем: «Выпуклый — имеющий дугообразную поверхность, обращённую наружу». А что значит дугообразную? Читаем: «Дугообразный — имеющий форму дуги». Что же такое дуга? — «Дуга — часть окружности, круга, или другой кривой линии». Тут уже наше терпение лопается: во-первых, кривые линии могут быть самыми разнообразными, а во-вторых, круг — не линия. Исходя из этого определения выпуклости, можно ли что-нибудь утверждать о выпуклости (или невыпуклости), например, куба? По-моему, нельзя. Так что такое «определение» никак не может устроить математика.
В математике понятие выпуклый имеет чётко определённый смысл. Множество точек называется выпуклым, если вместе с любыми двумя его точками
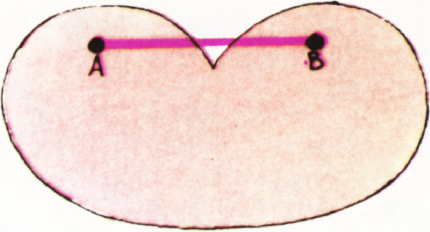
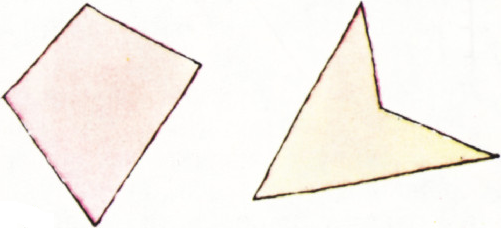
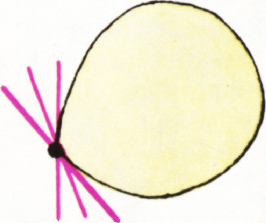
Теперь довольно очевидно, что куб — выпуклое тело. А вот фигура на рисунке 1 не выпукла. Нетрудно понять, что любой треугольник является выпуклой фигурой. А четырёхугольники могут быть как выпуклыми, так и невыпуклыми (рис. 2).
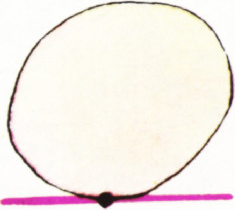
Ну, а можно ли про выпуклые множества что-нибудь доказать? Можно. Например, докажите (это совсем просто), что пересечение двух или нескольких выпуклых множеств снова является выпуклым множеством (пустое множество также будем считать выпуклым). Более трудно доказать такое утверждение: через любую точку границы выпуклой фигуры на плоскости можно провести прямую так, чтобы вся фигура лежала по одну сторону от этой прямой. Такая прямая изображена на рисунке З; она называется опорной прямой. Если граничная точка является «угловой», как на рисунке 4, через неё можно провести несколько опорных прямых. Докажите самостоятельно, что если некоторая плоская фигура имеет опорную прямую в каждой граничной точке, то эта фигура является выпуклой. Таким образом, сформулированное утверждение можно принять за определение выпуклой фигуры.
Думаю, что наличие опорных прямых у плоских выпуклых фигур (аналогично — опорных плоскостей у выпуклых тел), хотя и является очень важным свойством, вряд ли кого удивит: оно довольно очевидно. Следующий факт гораздо более удивителен.
Теорема. Если на плоскости задано несколько выпуклых фигур, каждые три из которых имеют общую точку, то найдётся точка, принадлежащая одновременно всем этим фигурам.
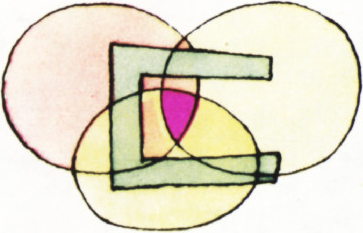
Требование выпуклости фигур существенно. Действительно, взгляните на рисунок 5: из четырёх фигур, изображённых на ней, невыпукла лишь одна; однако, хотя у любых трёх фигур есть общая точка, точки, принадлежащей одновременно всем четырём фигурам, нет.
А если на плоскости задано несколько выпуклых фигур, таких что любые две из них имеют общую точку? Обязательно ли найдётся точка, общая для всех этих фигур? Покажите самостоятельно, что такой точки может и не быть.
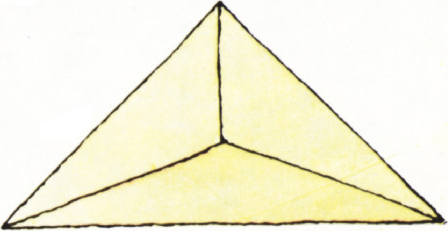
Вы обратили внимание, что мы всё время подчёркивали то, что рассматриваемые фигуры — плоские? И это неспроста, потому что существуют четыре выпуклых тела в пространстве, каждые три из которых имеют общую точку, но нет точки, общей всем четырём телам, например, четыре грани треугольной пирамиды, изображённой на рисунке 6. Значит, в пространстве подобная теорема уже не имеет места? Оказывается, чтобы она осталась верной и в пространстве, её достаточно лишь немного «подправить». А именно:
Теорема′. Если в пространстве задано несколько выпуклых тел, каждые четыре из которых имеют общую точку, то найдётся точка, принадлежащая одновременно всем этим телам.
Теорема, о которой мы только что рассказали, была открыта не так давно — в начале 20-х годов нашего столетия австрийским математиком Э. Хелли и носит его имя (Хелли сформулировал её для выпуклых тел, расположенных в
Теорема′′. Если на прямой задано несколько выпуклых множеств, каждые два из которых имеют общую точку, то найдётся точка, принадлежащая одновременно всем этим множествам.
Попробуйте доказать эту теорему самостоятельно.
Если вас заинтересовали выпуклые фигуры, прочтите книгу И. М. Яглома и В. Г. Бoлтянского, которая так и называется: «Выпуклые фигуры».


