Задача М953‍‍

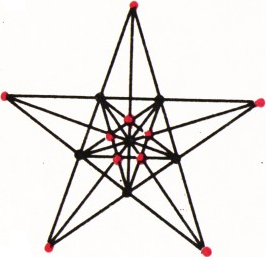
Ответ: 10 точек. Пример расположения с 10 точками тройного пересечения прямых показан на рисунке 1: за исходные 6 точек здесь берутся вершины и центр правильного пятиугольника.

Покажем теперь, что на каждой из 15 рассматриваемых прямых лежит не более двух точек тройного пересечения (отличных от данных), т. е. что общее их число не превосходит $\dfrac{15\cdot 2}3=10$‍‍ (при подсчёте учитывается, что каждая из этих точек лежит на трёх прямых).

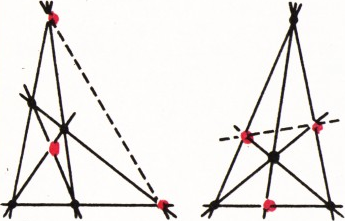
Заметим, что 6 прямых, попарно соединяющих любые 4 из данных точек, пересекаются по две в трёх точках (если среди этих прямых нет параллельных), причём эти три точки не могут лежать на одной прямой (рис. 2). Поэтому на прямой, соединяющей две оставшиеся точки, могут лежать самое большее две точки тройного пересечения, что и требовалось доказать.

Выделенное курсивом утверждение нетрудно доказать строго, пользуясь тем, что прямая, не проходящая через вершины треугольника и пересекающая одну из его сторон, пересекает ровно одну другую сторону‍. Интересно, что в некоторых неевклидовых геометриях это утверждение принимают за аксиому («аксиома Фано»), а в некоторых геометриях оно и вовсе не выполняется.