Задача М916‍‍

Обозначим вершины данного треугольника через $A$‍,‍ $B$‍,‍ $C$‍,‍ середины его сторон — $A_1$‍,‍ $B_1$‍,‍ $C_1$‍,‍ три другие вершины рассматриваемого в задаче шестиугольника — $A_2$‍,‍ $B_2$‍,‍ $C_2$‍‍ (см. рисунок). Заметим, что отрезки, соединяющие центр $O$‍‍ описанной окружности треугольника $ABC$‍‍ с серединами его сторон, разбивают наш шестиугольник на три параллелограмма $OA_1C_2B_1$‍,‍ $OB_1A_2C_1$‍‍ и $OC_1B_2A_1$‍‍ (отрезки $OA_1$‍‍ и $B_1C_2$‍‍ параллельны, так как оба они перпендикулярны стороне $BC$‍;‍ аналогично $OB_1\parallel A_1C_2$‍‍ и т. д.). Отсюда следует, что треугольники $A_1B_1C_2$‍,‍ $B_1C_1A_2$‍‍ и $C_1A_1B_2$‍‍ соответственно равны треугольникам $A_1B_1O$‍,‍ $B_1C_1O$‍‍ и $C_1A_1O$‍,‍ а значит, площадь шестиугольника вдвое больше площади треугольника $A_1B_1C_1$‍,‍ очевидно, равной четверти площади исходного треугольника.

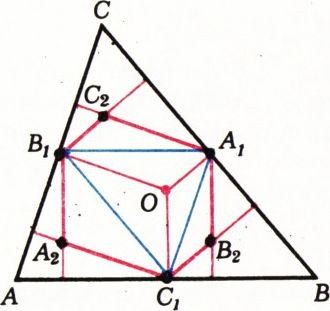
Другое доказательство опирается на то, что три высоты треугольника пересекаются в одной точке: $A_2$‍,‍ $B_2$‍‍ и $C_2$‍‍ — это точки пересечения высот равных треугольников $AB_1C_1$‍,‍ $C_1A_1B$‍‍ и $B_1CA_1$‍,‍ отсюда $\triangle A_2B_1C_1=\triangle C_2CA_1$‍,‍ $\triangle B_2A_1C_1=\triangle C_2CB_1$‍,‍ следовательно, наш шестиугольник равновелик параллелограмму $C_1A_1CB_1$‍.‍

Отметим, что в случае тупоугольного треугольника аналогичное построение приводит к самопересекающейся шестизвенной ломаной, для которой утверждение останется в силе, если рассматривать так называемую «ориентированную площадь» (см. статью А. Л. Тоома «Сколько площадей у многоугольника?»‍ в «Кванте» № 12 за 1984 г.).