Условие задачи (1984, № 9) Задача М881 // Квант. — 1984. — № 9. — Стр. 34; 1984. — № 12. — Стр. 36.
Докажите, что сумма расстояний от произвольной точки плоскости до трёх вершин равнобедренной трапеции больше расстояния от этой точки до четвёртой её вершины.
Изображения страниц
Решение задачи (1984, № 12) Задача М881 // Квант. — 1984. — № 9. — Стр. 34; 1984. — № 12. — Стр. 36.
Пусть, для определённости,
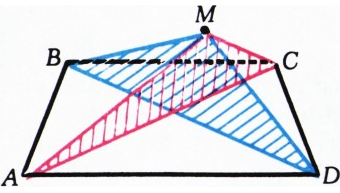
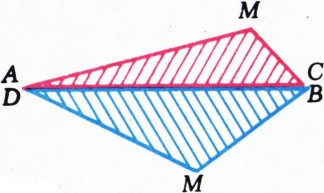
Это решение имеет красивую геометрическую интерпретацию: прикладывая друг к другу треугольники

