Задача М877 / Задачи // Архив журнала «Квант»

Условие задачи (1984, № 8) Задача М877 // Квант. — 1984. — № 8. — Стр. 44; 1984. — № 11. — Стр. 39.

Из листа клетчатой бумаги размерами $29\times 29$‍‍ клеток вырезали 99 квадратиков размерами $2\times 2$‍‍ каждый. Докажите, что из него можно вырезать ещё один такой квадратик.

С. В. Фомин

Ленинградская городская математическая олимпиада (50, 1984 год)

Открыть в номере

Изображения страниц

‍

Скачать PDF

Решение задачи (1984, № 11) Задача М877 // Квант. — 1984. — № 8. — Стр. 44; 1984. — № 11. — Стр. 39.

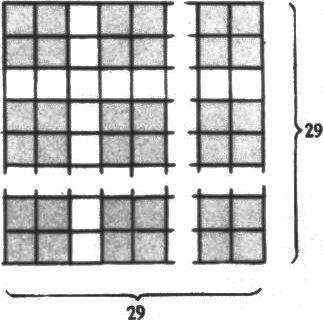
На рисунке серым цветом закрашены 100 квадратиков $2\times2$‍.‍ Вырезая из исходного квадрата $29\times29$‍‍ любой квадратик $2\times2$‍,‍ мы «задеваем» ровно один серый квадратик. Следовательно, после 99 таких операций один из серых квадратиков останется нетронутым.

С. В. Фомин

Открыть в номере

Метаданные Задача М877 // Квант. — 1984. — № 8. — Стр. 44; 1984. — № 11. — Стр. 39.

Предмет

Математика

Условие

Фомин С. В.

Решение

Фомин С. В.

Номера

1984. — № 8. — Стр. 44 [условие]

1984. — № 11. — Стр. 39 [решение]

Описание

Задача М877 // Квант. — 1984. — № 8. — Стр. 44; 1984. — № 11. — Стр. 39.

Ссылка

https://www.kvant.digital/problems/m877/