Задача М818‍‍

Пусть какие-то $k$‍‍ вершин правильного $n$‍‍-угольника закрашены синим цветом (остальные вершины — чёрные). Будем называть множество закрашенных вершин равномерным, если при любом $m$‍‍ количества синих вершин в любых двух наборах из $m$‍‍ последовательных вершин $n$‍‍-угольника совпадают или отличаются на 1 (см. рис. 1, где приведён пример равномерного множества для $n=8$‍,‍ $k=5$‍).‍

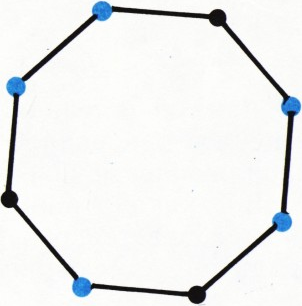
1. Постройте равномерные множества для $n=12$‍,‍ $k=5$‍;‍ $n=17$‍,‍ $k=7$‍.‍

Докажите, что равномерное множество существует и единственно (с точностью до поворотов $n$‍‍-угольника),

2. если $n$‍‍ делится на $k$‍;‍
3. для любых $n$‍‍ и $k$‍‍ ($k\le n$‍).‍