Условие задачи (1970, № 2) Задача М8 // Квант. — 1970. — № 2. — Стр. 47; 1970. — № 10. — Стр. 38—42.
Двое играют в такую игру. Из кучки, где имеется 25 спичек, каждый берёт себе по очереди одну, две или три спички. Выигрывает тот, у кого в конце игры — после того, как все спички будут разобраны, — окажется чётное число спичек.
Кто выигрывает при правильной игре — начинающий или его партнёр? Как он должен играть, чтобы выиграть? Как изменится ответ, если считать, что выигрывает забравший нечётное число спичек?
Исследуйте эту игру в общем случае, когда спичек
Изображения страниц
Решение задачи (1970, № 10) Задача М8 // Квант. — 1970. — № 2. — Стр. 47; 1970. — № 10. — Стр. 38—42.
Для того чтобы говорить об игре, необходимо как-то назвать её участников. Условимся раз навсегда называть одного из них Я, а другого Он.
Прежде всего немного обобщим условие задачи. Число
Мы рассматриваем, строго говоря, сразу бесконечное число игр, так как
Будем говорить сначала обо всех вариантах этой игры вместе.
Давайте подумаем о том, что надо помнить игроку в ходе игры. Надо ли ему помнить все его ходы и ходы его противника с начала игры? Нет, в любом варианте ему достаточно знать следующее:
- сколько осталось спичек на столе,
- чётное ли у него число спичек,
- чей ход.
Если заданы эти три параметра, то мы будем говорить, что задано
состояние игры. В каждом таком состоянии игрок может сделать
Состояния игры удобно изображать на бумаге в виде клеточек или кружочков, а возможные ходы в виде стрелок. Так мы и сделаем.
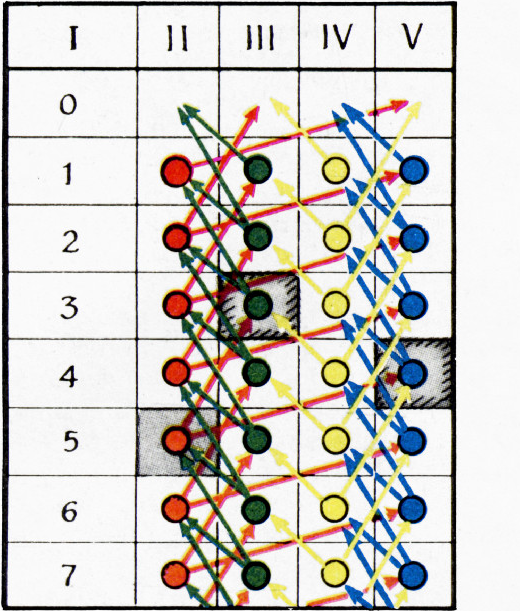
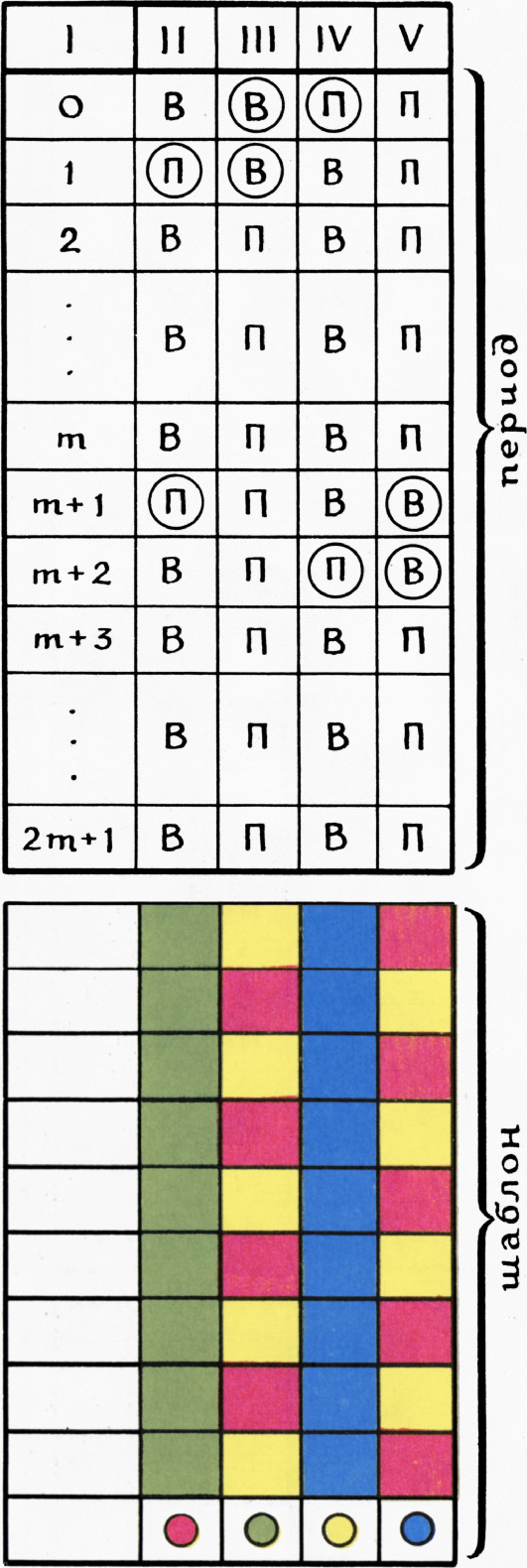
Рис. 1. Таблица возможных состояний и ходов игры с
В таблицах на рисунках 1—4:
I столбец — номер строки
II столбец — у меня чётное число спичек, мой ход;
III столбец — у меня чётное число спичек, его ход;
IV столбец — у меня нечётное число спичек, мой ход;
V столбец — у меня нечётное число спичек, его ход.
Таблица на рисунке 1 составлена для случая, когда
Цветные стрелки показывают, как игроки могут ходить: игрок, чей ход в этой клетке, может пойти по любой стрелке, из неё выходящей. Например, первая слева клетка в строчке с номером 5 (серая) соответствует тому состоянию игры, когда на столе осталось 5 спичек, у меня чётное число спичек и мой ход, а две выходящие из этой клетки стрелки показывают, в какие состояния Я могу перевести игру очередным ходом.
Таблицу можно продолжать вниз сколько угодно далеко. Стрелки, выходящие из любой клетки, получаются параллельным сдвигом из стрелок, выходящих из какой-то одной клетки того же самого столбца (в верхних двух клетках некоторые стрелки, разумеется, «выпадают»).
Назовём состояние выигрышным и поставим в соответствующую ему клетку букву В, если, когда игра начинается из этого состояния, Я могу выиграть, как бы Он ни старался мне помешать.
Назовём состояние проигрышным и поставим в соответствующую ему клетку букву П, если, когда игра начинается из этого состояния, Он может выиграть и, если Он не ошибётся, Я не смогу этому воспрепятствовать.
Приступим теперь к основной части решения: расставим во все клетки таблицы буквы В и П. Мы сделаем это сначала для игры, соответствующей рисунку 1. В нулевой строке буквы, конечно, надо поставить так: ВВПП, поскольку мы считаем, что Я выиграл, если в конце игры у меня чётное число спичек. Дальше буквы надо расставлять сверху вниз по следующему закону.
I. Если мой ход (т. е. клетка находится во II или IV столбце), то в неё ставится:
буква В, если хоть одна стрелка из неё ведёт в клетку с буквой В;
буква П, если всякая стрелка, выходящая из неё, ведёт в клетку с буквой П.
II. Если его ход (т. е. клетка находится в III или V столбце), то в неё ставится:
буква П, если хоть одна стрелка из неё ведёт в клетку с буквой П;
буква В, если всякая стрелка, выходящая из неё, ведёт в клетку с буквой В.
Поскольку все стрелки в таблице ведут снизу вверх, то этот закон даёт возможность заполнять всю таблицу, сколько бы мы её ни продолжали.
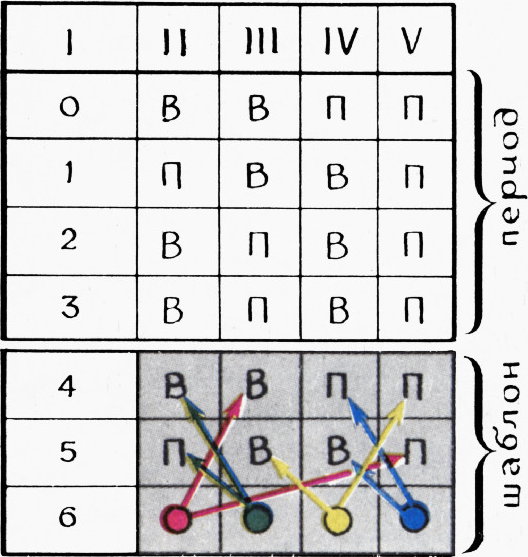
В нашем случае
На самом деле, дальше пятой строки таблицу заполнять не нужно. Дело в том, что 4-я строка совпадает с нулевой, а 5-я с первой. Поэтому 6-я обязательно совпадёт со 2-й (так как каждая строка определяется двумя предыдущими). Тогда 7-я строка совпадёт с 3-й, 8-я с 4-й, 9-я с 5-й и т. д. Строки будут повторяться с периодом 4, откуда следует, что всякая
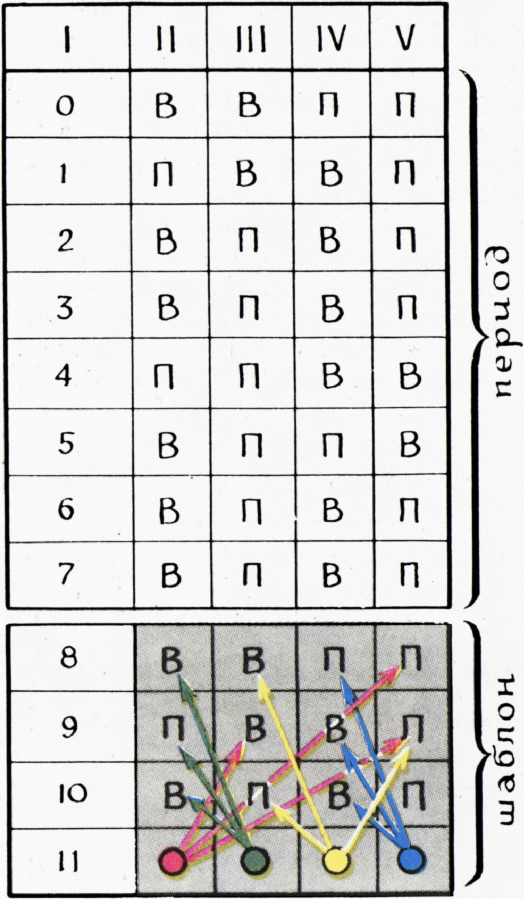
строка с номером
строка с номером
строка с номером
строка с номером
В частности, 25-я строка будет ПВВП
То, что период обязательно должен быть, можно было предвидеть заранее. Действительно, пусть мы заполнили таблицу до какой-то строки. Дальше всё зависит от того, как заполнены две последние строки. Число всех способов заполнить две строки буквами П и В конечно (оно заведомо не больше 28). Значит, при заполнении таблицы не может всё время появляться новая пара строк. А когда какая-то пара строк повторится, начнётся периодичность.
После того как в таблице расставлены буквы В и П, становится ясной и стратегия, которой Я должен придерживаться, чтобы выиграть: нужно каждый раз делать такой ход, который ведёт в клетку с буквой В. Закон расстановки букв В и П, указанный выше, составлен именно так, что если Я один раз попал в клетку В, то дальше Я смогу каждый раз ходить в В, и противник не сможет мне помешать.
Случай, когда Я выигрываю, если у меня в конце нечётное количество спичек, исследуется аналогично. Можно поставить в нулевой строке ППВВ и заполнять дальше таблицу по тому же самому закону. Период снова будет равен 4. Но можно всего этого и не делать, а использовать для этого случая тот же рисунок 2.
Заметим, что не дать игроку перед началом игры ничего и потребовать,
чтобы у него в конце было нечётное число спичек, это всё равно, что дать ему перед началом игры одну спичку и потребовать, чтобы у него в конце игры было
чётное число спичек. Таким образом, в этом новом случае Я
выигрываю, если в таблице на рисунке 2 в клетке на пересечении
IV столбца стоит В, если Я начинаю,
V столбца стоит В, если Он начинает.
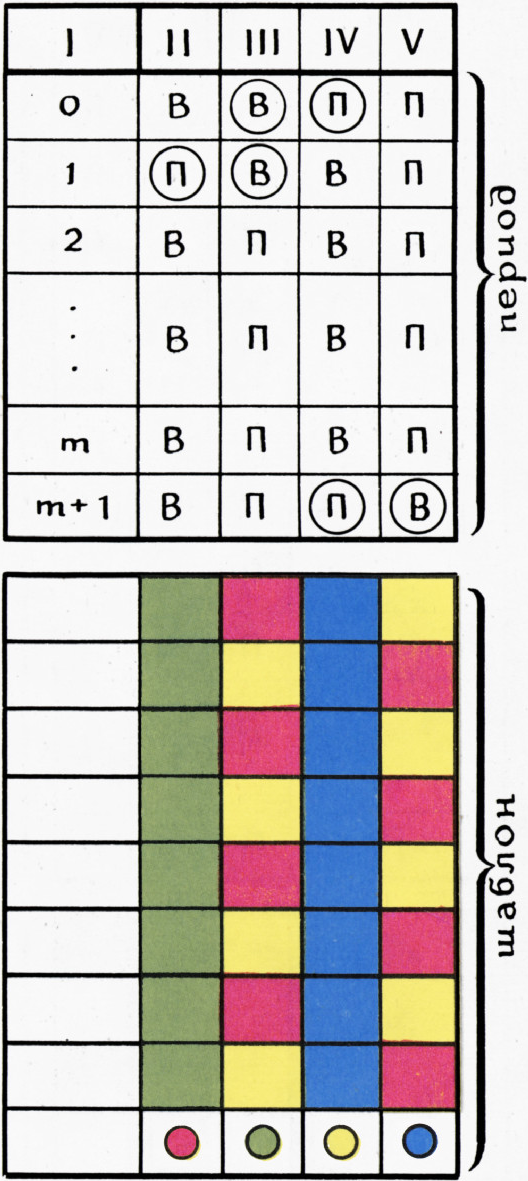
Заметим также, что шаблон не изменится, если поменять
местами II столбец с IV, а III с V. В первой строке после такой перестановки
вместо ВВПП будет стоять ППВВ. Поэтому таблицу для того случая, когда Я, чтобы выиграть, должен забрать нечётное число спичек, можно получить из таблицы для разобранного случая указанной перестановкой столбцов. Это же относится и ко всем другим значениям
Пусть теперь
Таким образом, в случае
Ответ: если выигравшим считается игрок, забравший чётное число спичек, то начинающий проигрывает, а если выигравшим считается забравший нечётное число спичек, то начинающий выигрывает.
Общий случай исследуется аналогично. Длина периода оказывается равной
Как видим, при больших





