Условие задачи (1982, № 6) Задача М750 // Квант. — 1982. — № 6. — Стр. 20; 1982. — № 12. — Стр. 21—22.
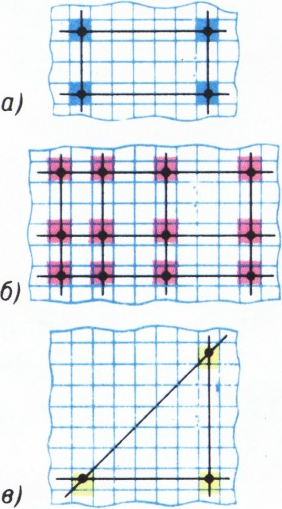
Докажите, что, как бы ни раскрасить клетки бесконечного листа клетчатой бумаги в
- прямоугольник, вершины которого лежат в центрах клеток одного цвета (а стороны идут параллельно линиям сетки — по вертикальным и горизонтальным прямым — рис. 3, а);
$l$ горизонтальных и$m$ вертикальных прямых, которые пересекаются в центрах$lm$ клеток одного цвета($l$ и$m$ — любые натуральные числа — рис. 3, б);- равнобедренный прямоугольный треугольник, вершины которого — центры клеток одного цвета, при
$N=2$ (рис. 3, в); - то же для
$N=3$.
Изображения страниц
Решение задачи (1982, № 12) Задача М750 // Квант. — 1982. — № 6. — Стр. 20; 1982. — № 12. — Стр. 21—22.
В решении мы многократно используем «принцип Дирихле».
а) Этот пункт — частный случай следующего.
б) Рассмотрим горизонтальную полосу бумаги ширины
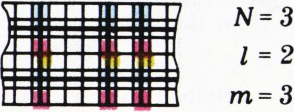
Так как каждый из выбранных столбцов окрашен в
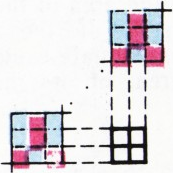
в) Пусть клетки окрашены в красный и синий цвета. Рассмотрим цепочку попарно не пересекающихся квадратов
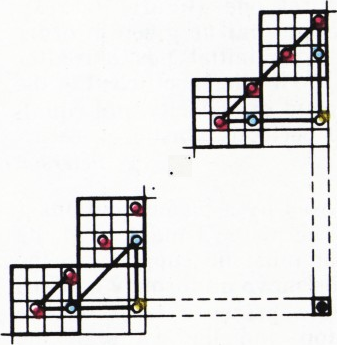
г) Будем рассуждать аналогично с решением пункта в). Рассмотрим бесконечную цепочку достаточно больших квадратов, расположенных по диагонали (что значит «достаточно большой» — выяснится ниже). Среди них всегда найдутся два одинаково раскрашенных. Пусть сторона большого квадрата настолько велика, что вдоль его диагонали можно поместить больше квадратов
Эта задача тесно связана с так называемой «теоремой Ван-дер-Вардена о прогрессиях», о которой мы расскажем в одном из ближайших номеров.


