Задача М748‍‍‍

а) Проведём произвольную прямую, не параллельную ни одной из осей парабол. Такая прямая может пересекаться с внутренней областью любой из парабол только по интервалу. В самом деле, уравнение параболы в некоторой системе координат имеет вид $y=ax^2$‍‍ ($a\gt0$‍),‍ а уравнение прямой — $y=kx+l$‍;‍ абсциссы точек прямой, принадлежащих внутренности параболы, удовлетворяют неравенству $kx+l\gt ax^2$‍,‍ множество решений которого либо пустое, либо — интервал $x_1\lt x\lt x_2$‍,‍ где $x_1$‍‍ и $x_2$‍‍ — корни уравнения $ax^2-kx-l=0$‍.‍ Отсюда следует, что на проведённой прямой найдутся точки, не принадлежащие ни одной из внутренних областей парабол.

б) Пусть $O$‍‍ — произвольная точка пространства и $K'$‍‍ — конус, полученный из конуса $K$‍‍ с вершиной $Q$‍‍ параллельным переносом, переводящим точку $Q$‍‍ в точку $O$‍.‍ Проведём произвольный луч $l$‍‍ с началом в точке $O$‍.‍ Рассмотрим сечения конусов $K$‍‍ и $K'$‍‍ плоскостью, проходящей через луч $l$‍‍ и точку $Q$‍‍ (рис. 1). Она пересекает конусы по двум углам с параллельными сторонами; пользуясь этим, легко убедиться, что луч $l$‍‍ пересекается с конусом $K$‍‍ по лучу тогда и только тогда, когда он целиком содержится в конусе $K'$‍.‍ В противном случае луч $l$‍‍ пересекается с конусом $K$‍‍ по отрезку или по одной точке $Q$‍‍ или вовсе не пересекается.

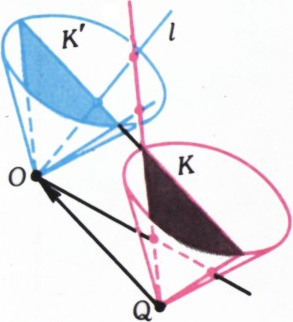
Перенесём теперь вершины всех конусов в точку $O$‍‍ и докажем, что никакие два конуса полученного «букета» не имеют общих точек, кроме точки $O$‍.‍

Предположим, что это не так, и какие-то два конуса $K'_1$‍‍ и $K'_2$‍‍ имеют общую точку $A\ne O$‍.‍ Тогда луч $l=[OA)$‍‍ содержится в каждом из них. Как было показано, в этом случае луч $l$‍‍ пересекается с конусом $K_1$‍‍ по некоторому лучу $l_1$‍,‍ а с конусом $K_2$‍‍ — по лучу $l_2$‍.‍ Но тогда точки луча $l_1\cap l_2$‍‍ принадлежат обоим конусам $K_1$‍‍ и $K_2$‍.‍ Противоречие.

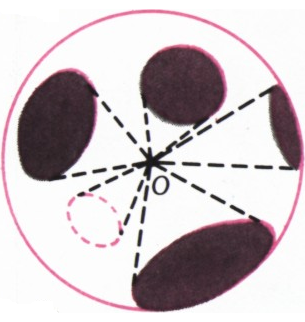
Рассмотрим теперь сферу с центром в точке $O$‍.‍ С каждым из конусов «букета» она пересекается по некоторой «сферической шапочке» (рис. 2). Так как все такие «шапочки» попарно не пересекаются, их суммарная площадь меньше площади сферы. Поэтому, как бы мы их ни перемещали по сфере, покрыть ими всю сферу невозможно. Это значит, что при любом расположении конусов в пространстве на сфере найдутся точки, не покрытые «шапочками». Если $A$‍‍ — такая точка, то луч $[OA)$‍‍ может пересекаться с конусами только по конечному числу отрезков. Поэтому на этом луче заведомо найдутся точки, не принадлежащие ни одному из конусов.

Автор задачи М748 А. Кузьминых и некоторые другие читатели обратили внимание на неточности в изложении решений этой задачи. Приведём краткое решение, в котором более чётко выделена основная идея. Речь идёт о таком утверждении (пункт б) задачи): если несколько конусов в пространстве попарно не пересекаются, то их нельзя передвинуть так, чтобы они покрыли всё пространство. (Здесь конус — тело, полученное вращением угла, меньшего развёрнутого, вокруг биссектрисы.)

Идея решения — рассмотреть множество всех направлений в пространстве. Будем каждому направлению сопоставлять луч с началом в фиксированной точке $O$‍.‍ Ещё лучше: возьмём сферу (скажем, радиуса 1) с центром в точке $O$‍‍ — каждой её точке $M$‍‍ отвечает определённое направление $OM$‍‍ в пространстве. Каждому конусу $K$‍‍ отвечает «шапочка» на сфере — пересечение сферы с конусом $K_O$‍,‍ полученным из $K$‍‍ параллельным переносом вершины в точку $O$‍;‍ при этом для любой точки $M$‍‍ внутри $K_O$‍‍ луч направления $OM$‍‍ пересекает конус $K$‍‍ по некоторому лучу, а для точки $M$‍‍ вне $K_O$‍‍ — на более чем по отрезку (быть может, вовсе не пересекает $K$‍);‍ чтобы убедиться в этом, полезно провести плоскость через луч $OM$‍‍ и вершину конуса $K$‍.‍ Если два конуса в пространстве не пересекаются, то соответствующие им шапочки на сфере направлений также не могут иметь общих внутренних точек: для такой точки $M$‍‍ луч $OM$‍‍ должен был бы пересекаться с каждым из двух конусов по лучу, т. е. конусы должны были бы иметь общий луч. Таким образом, шапочки для данных в условии конусов в сумме имеют площадь, меньшую площади сферы, поэтому как бы мы ни двигали конусы, шапочки не смогут покрыть сферу. Но для любой непокрытой ими точки $M$‍‍ луч $OM$‍‍ пересекается с каждым из (передвинутых) конусов не более чем по отрезку, так что конусы не покрывают пространство.