Условие задачи (1981, № 5) Задача М683 // Квант. — 1981. — № 5. — Стр. 20; 1982. — № 1. — Стр. 27—28.
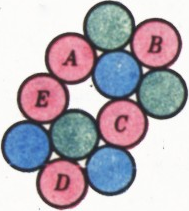
Несколько кружков одинакового размера положили на стол так, что никакие два не перекрываются. Докажите, что кружки можно раскрасить в четыре цвета так, что любые два касающихся кружка будут окрашены в разные цвета. Найдите расположение кружков, при котором трёх цветов для такой раскраски недостаточно.
Изображения страниц
Решение задачи (1982, № 1) Задача М683 // Квант. — 1981. — № 5. — Стр. 20; 1982. — № 1. — Стр. 27—28.
Доказательство возможности требуемой раскраски проведём индукцией по числу кружков
При
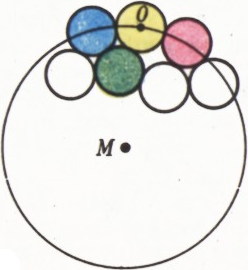
Отбросим кружок с центром
Утверждение доказано.
На рисунке 2 изображены 11 кружков, для нужной раскраски которых трёх цветов недостаточно. Действительно, предположив, что эти кружки можно раскрасить тремя цветами, получим, что кружки