Задача М627‍‍‍

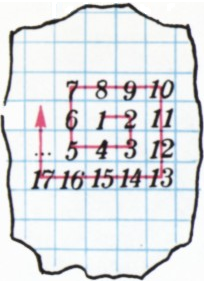
Пример расстановки чисел, удовлетворяющей условию а), изображён на рисунке 1.

Докажем утверждение задачи а). Возьмём на нашем листе клетчатой бумаги произвольный квадрат размером $2m\times2m$‍‍ ($m\gt1$‍)‍ клеток. В клетках этого квадрата стоит $4m^2$‍‍ различных чисел, так что наибольшее из них отличается от наименьшего по крайней мере на $4m^2-1$‍.‍ Соединим теперь клетки, в которых стоят наибольшее и наименьшее числа, «дорожкой», как показано на рисунке 2. Длина этой «дорожки» не превосходит $4m-1$‍,‍ и поэтому хотя бы некоторые из разностей соседних на этой «дорожке» чисел не меньше $\dfrac{4m^2-1}{4m-1}$‍,‍ т. е. больше $m$‍.‍

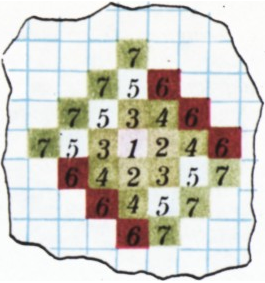
На рисунке 3 натуральные числа расположены так, что каждое число $n\in\mathbb{N}$‍‍ встречается ровно $n$‍‍ раз и разности чисел в соседних клетках не превосходят 2. Уменьшить $k+1=2$‍‍ нельзя уже потому, что рядом с единицей — четыре клетки, а двоек только две, так что две из соседних с единицей клеток придётся заполнить тройками.

Таким образом, искомое $k$‍‍ равно 2.

Попробуйте разобраться самостоятельно в следующих вопросах:

1. Можно ли расставить числа в клетках бесконечного листа клетчатой бумаги так, чтобы разности чисел, стоящих в соседних клетках, не превосходили 1, если каждое число $n\in\mathbb{N}$‍‍ встречается $n^2$‍‍ раз? А $n+100$‍‍ раз?
2. Пусть пространство разбито на кубические ящички, и в каждый ящичек помещено натуральное число так, что каждое число $n\in\mathbb{N}$‍‍ встречается ровно $n$‍‍ раз. Каким будет ответ на вопрос, аналогичный вопросу задачи М627?