Задача М610‍‍

Как известно, если два множества имеют одинаковое число элементов, между ними можно установить взаимно однозначное соответствие. Собственно говоря, это и есть определение того, что в множествах элементов поровну, но этот факт иногда забывается. А между тем довольно часто равенство двух чисел устанавливается именно через взаимно однозначное соответствие подходящих множеств.

Нам нужно доказать, что наборов, в которых $a_k=k$‍,‍ ровно половина. Поэтому попробуем установить взаимно однозначное соответствие между этими наборами и оставшимися теми, у которых $a_k\lt k$‍.‍

Сопоставить набору $(a_1,a_2,\ldots,a_k)$‍‍ набор $(a_k,a_{k-1},\ldots,a_1)$‍‍ нельзя, так как новый набор — невозрастающий. Можно попробовать сопоставить набору $(a_1,\ldots,a_k)$‍‍ набор $(k-a_k,k-a_{k-1},\ldots,k-a_1)$‍:‍ он уже — неубывающий, но... $k-a_1$‍‍ не обязано быть меньше $k$‍.‍ Поэтому это соответствие не решает задачу. (Вопрос: какую задачу решает это соответствие?)

Значит, необходимо более сложное соответствие. Для его построения нам понадобится понятие диаграммы Юнга данного набора.

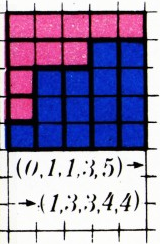
Что это такое, проще всего объяснить на примере: набору $(0,0,2,3,5)$‍‍ соответствует диаграмма, изображённая на рисунке 2 — в каждой строке столько квадратиков, каково соответствующее число.

Дополним диаграмму Юнга до квадрата (рис. 3). Тогда становится ясно, что наша первоначальная идея заключалась в том, чтобы отсчитывать диаграмму не из красных, а из белых квадратиков (и, соответственно, не слева-снизу, а справа-сверху).

Попытаемся теперь дополнить рисунок 3 вертикальной диаграммой — как на рисунке 4. Отсчитывая эту диаграмму снизу-слева, получим набор $(2,2,3,4,4)$‍.‍ Назовём этот набор дополнительным к набору $(0,0,2,3,5)$‍.‍

Ещё один пример изображён на рисунке 5.

Ясно, что если исходный набор $(a_1,\ldots,a_k)$‍,‍ а дополнительный — $(b_1,\ldots,b_k)$‍,‍ то $a_k=k$‍‍ тогда и только тогда, когда $b_k\lt k$‍.‍ В самом деле, $a_k=k$‍,‍ если верхняя правая клетка входит в основную диаграмму Юнга, и $a_k\lt k$‍,‍ если она входит в дополнительную.

Установленное нами соответствие между наборами, у которых $a_k=k$‍,‍ и наборами, у которых $a_k\lt k$‍,‍ очевидно, взаимно однозначно. Тем самым мы решили а). Кроме того, сумма чисел исходного и дополнительного наборов равна $k^2$‍‍ (в наших примерах — 25). Поэтому сумма чисел дополнительного набора делится на $k$‍‍ тогда и только тогда, когда делится на $k$‍‍ сумма чисел исходного набора. Это решает б).

Замечание. Задача а) имеет и другое решение: можно непосредственно посчитать числа $N$‍‍ и $M$‍.‍ Именно:

Лемма. Число наборов целых чисел $a_1$‍,‍ $\ldots$‍,‍ $a_m$‍‍ таких, что $0\le a_1\le\ldots\le a_m \le k$‍,‍ равно $C^m_{k+m}$‍.‍

Доказательство. Рассмотрим набор $(b_1,\ldots,b_m)$‍,‍ где $b_i=a_i+i$‍:‍ $b_1=a_1+1$‍,‍ $b_2=a_2+2$‍‍ и т. д. Тогда, очевидно, $1\lt b_1\lt b_2\lt\ldots\lt b_m\le k+m$‍,‍ т. е. $(b_1,\ldots,b_m)$‍‍ — произвольный возрастающий набор $m$‍‍ целых чисел их первых $k+m$‍‍ чисел. Число таких наборов равно $C^m_{k+m}$‍.‍

Поэтому число наборов, в которых $a_k\le k$‍,‍ по лемме равно $C^k_{2k}$‍.‍ Если же $a_k=k$‍,‍ то нам остаётся выбрать числа $a_1$‍,‍ $\ldots$‍,‍ $a_{k-1}$‍‍ так, что $0\le a_1\le\ldots\le a_{k-1}\le k$‍;‍ их число равно $C^{k-1}_{2k-1}$‍.‍ Остаётся посчитать, что $2C^{k-1}_{2k-1}$‍‍ равно $C^k_{2k}$‍.‍