Задача М6‍‍

Ответ. Таких положений существует 132. Другими словами, существует 66 пар расположений стрелок таких, что в каждой из этих пар одно расположение получается из другого заменой часовой стрелки на минутную и минутной на часовую (как на рис. 1); разумеется, при этом не рассматриваются такие положения, когда направления часовой и минутной стрелок совпадают: в этих случаях время определяется однозначно.

Решение. Мы получили много разных решений этой задачи. Приведём некоторые из них. Вот наиболее распространённое.

Будем считать, что циферблат разбит на 12 частей. Рассмотрим какое-то одно из положений стрелок, о которых идёт речь в условии. Пусть одна стрелка занимает положение $x$‍,‍ другая — $y$‍;‍ здесь $0\le x\lt 12$‍,‍ $0\le y\lt 12$‍.‍ Если первую стрелку считать часовой, а вторую — минутной, то должно выполняться равенство $$ x=a+\dfrac{5y}{60},\tag1 $$ где $a$‍‍ — целое число часов, $0\le a\le 11$‍.‍

Аналогично, если первая стрелка минутная, а вторая — часовая, то $$ y=b+\dfrac{5x}{60},\tag2 $$ где $b$‍‍ — целое, $0\le b\le 11$‍.‍

Систему из двух равенств (1) и (2) можно заменить на эквивалентные: $$ \left\{\begin{array}{l} 12x=12a+y,\\ 12y=12b+x, \end{array}\right. \quad \left\{\begin{array}{l} 12x-12a=y,\\ 143x=12(b+12a), \end{array}\right. \quad \left\{\begin{array}{l} x=12\cdot\dfrac{b+12a}{143},\\[9pt] y=12\cdot\dfrac{a+12b}{143}. \end{array}\right. $$ Здесь $0\le a\le11$‍,‍ $0\le b\le11$‍‍ — целые числа. Каждая пара $(x,y)$‍,‍ удовлетворяющая этой системе, является её решением. Их всего $12^2=144$‍.‍ Ясно, что случаи, когда $x=y$‍,‍ т. е. когда $a=b$‍,‍ нужно исключить. Остаётся 132.

Два из них — соответствующие $a=2$‍,‍ $b=5$‍‍ и $a=5$‍,‍ $b=2$‍‍ — изображены на рисунке 1 (ясно, что замена $a$‍‍ на $b$‍‍ и $b$‍‍ на $a$‍‍ соответствует замене стрелок).

Очень наглядное решение прислал ученик 10 класса С. Поздняков (г. Вильнюс). Вот его рассуждения.

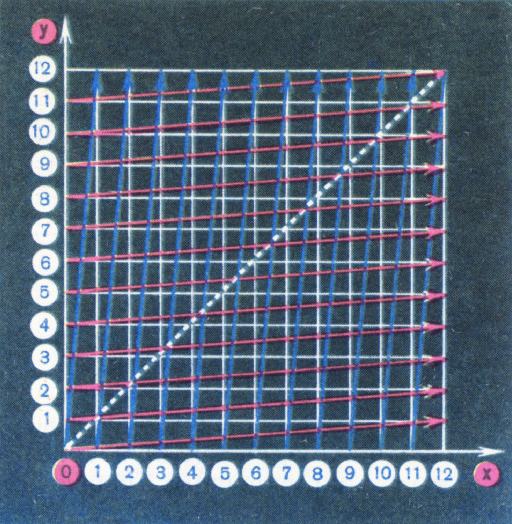
Зададим положение минутной стрелки $y$‍‍ как функцию от положения часовой стрелки $x$‍.‍ График этой функции $x\to y$‍‍ изображен на рисунке 2 синим цветом. Этот график — множество всех положений стрелок $(x,y)$‍,‍ которые могут встретиться на циферблате часов. Нас интересуют такие пары $(x,y)$‍,‍ для которых пара $(y,x)$‍‍ тоже принадлежит этому множеству. Но точка $(y,x)$‍‍ — это точка, симметричная $(x,y)$‍‍ относительно биссектрисы угла $xOy$‍.‍ На рисунке 2 множество точек, симметричных синим точкам, отмечено красным цветом‍.

Остаётся найти число точек пересечения синих и красных отрезков (не считая точек, лежащих на биссектрисе $x=y$‍).‍ Легко видеть, что их 132, т. е. 66 пар точек, симметричных относительно биссектрисы.

И, наконец, ещё одно, третье решение, не требующее никакого математического аппарата.

Положим рядом с нашими часами (справа) другие, воображаемые, которые идут ровно в 12 раз быстрее. Пустим и те и другие часы одновременно, когда они показывают 12 часов; тогда часовая стрелка правых часов всё время совпадает с минутной левых. Ясно, что интересующие нас «неразличимые» положения стрелок — в точности те, когда часовая стрелка левых совпадает с минутной правых, быстрых часов (подумайте, почему!). Сколько же раз это произойдёт? Из 144 оборотов, которые сделает минутная стрелка правых часов за то время, пока часовая стрелка «нормальных» сделает один оборот, на каждом обороте произойдёт одно совпадение (включая начальную точку первого оборота); из них нужно исключить 12 случаев, когда совпадают все четыре стрелки, — остаётся 132.