Задача М566‍‍

Мы приведём два решения этой задачи: в одном из них фиксируется внешний (больший) треугольник и меняется внутренний (меньший) — так поступило большинство наших читателей, правильно решивших эту задачу; в другом — наоборот: фиксируется внутренний треугольник, а меняется внешний.

Первое решение. Пусть длина катета внешнего (фиксированного) треугольника равна $a$‍;‍ найдём минимум площади $S$‍‍ внутреннего треугольника. Обозначим длину его катета через $u$‍.‍

Рассмотрим два случая:

1. вершина $C$‍‍ прямого угла внутреннего треугольника лежит на катете внешнего треугольника (рис. 1);
2. вершина $C$‍‍ внутреннего треугольника ($\widehat C=90^\circ$‍)‍ лежит на гипотенузе внешнего треугольника (рис. 2).

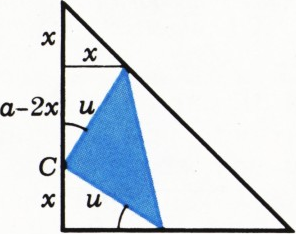
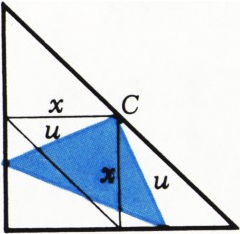
Для случая а) $$ \begin{gather*} S=\dfrac12u^2=\dfrac12\left(x^2+(a-2x)^2\right)=\dfrac12(5x^2-4ax+a^2)=\\ =\dfrac12\left[5\left(x-\dfrac{2a}5\right)^2+\dfrac{a^2}5\right], \end{gather*} $$ так что минимальное значение $S_{\text{min}}=\dfrac{a^2}{10}$‍‍ $\Big($‍‍при $\left(x-\dfrac{2a}5\right)^2=0\Big)$‍,‍ откуда наименьшее значение отношения площадей $$ k=\dfrac{\dfrac{a^2}{10}}{\dfrac{a^2}2}=\dfrac15. $$

В случае б) из рисунка 2 видно, что $u\ge x=\dfrac a2$‍;‍ поэтому в этом случае $S_{\text{min}}=\dfrac12\left(\dfrac a2\right)^2=\dfrac{a^2}8$‍,‍ откуда наименьшее отношение площадей равно $\dfrac14$‍.‍ Так как $\dfrac15\lt\dfrac14$‍,‍ искомое наименьшее значение равно $\dfrac15$‍.‍

Второе решение. Зафиксируем теперь меньший (внутренний) треугольник и будем менять больший (внешний) треугольник. Обозначим длину катета внутреннего треугольника через $a$‍,‍ длину катета внешнего — через $x$‍.‍

Вершины $A$‍,‍ $C$‍,‍ $B$‍‍ внешнего треугольника ($\widehat A=45^\circ$‍,‍ $\widehat C=90^\circ$‍,‍ $\widehat B=45^\circ$‍)‍ лежат на дугах, построенных на катетах и на гипотенузе внутреннего треугольника, вмещающих, соответственно, углы в $45^\circ$‍,‍ $90^\circ$‍‍ и $45^\circ$‍.‍ Снова возможны два случая:

1. вершины $A$‍‍ и $C$‍‍ внешнего треугольника лежат на дугах, построенных на катетах внутреннего треугольника (рис. 3);
2. вершины $A$‍‍ и $C$‍‍ внешнего треугольника лежат на дугах, построенных на катете и гипотенузе внутреннего треугольника (рис. 4).

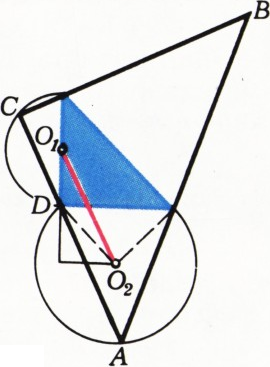
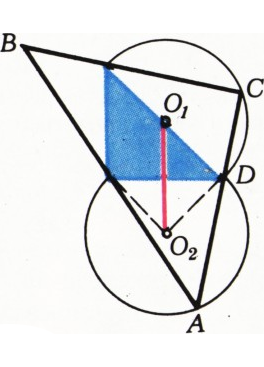
Поскольку площадь внешнего треугольника $S=\dfrac12x^2$‍‍ и отношение площадей $\dfrac{a^2}{x^2}$‍‍ минимально, когда $x$‍‍ — максимально, задача сводится к отысканию наибольшей общей хорды $AC$‍‍ двух пересекающихся окружностей, проходящей через точку $D$‍‍ их пересечения.

Из рисунка 5 видно, что $|AC|=2|O_1E|\le2|O_1O_2|$‍‍ ($O_1$‍‍ и $O_2$‍‍ — центры окружностей); следовательно, хорда наибольшей длины, проходящая через точку пересечения окружностей $D$‍,‍ параллельна отрезку, соединяющему центры упомянутых окружностей, и вдвое длиннее его.

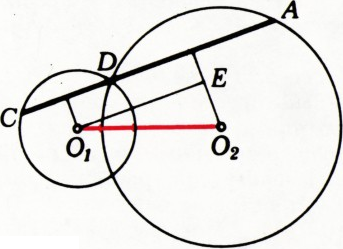
Для случая а) $$ x_{\text{max}}=2\sqrt{a^2+\dfrac{a^2}4}=a\sqrt5, $$ так что наименьшее отношение площадей $\dfrac{a^2}{x^2_{\text{max}}}=\dfrac15$‍.‍

Для случая б) $$ x_{\text{max}}=2a, $$ так что наименьшее отношение площадей равно $\dfrac14$‍.‍

Как и раньше, делаем вывод, что искомое наименьшее отношение площадей равно $\dfrac15$‍.‍

Второе решение, конечно, длиннее первого; но оно основано на красивом геометрическом рассуждении, которое можно применять и в других ситуациях. Например, когда рассматриваются произвольные треугольники. В этом вы можете убедиться, решив самостоятельно такую задачу:

В данный треугольник $ABC$‍‍ вписать подобный ему треугольник $A_1B_1C_1$‍‍ ($\widehat A=\widehat A_1$‍,‍ $\widehat B=\widehat B_1$‍,‍ $\widehat C=\widehat C_1$‍)‍ так, что $A_1\in[BC]$‍,‍ $B_1\in[CA]$‍,‍ $C_1\in[AB]$‍‍ и площадь треугольника $A_1B_1C_1$‍‍ — наименьшая. Более общая задача уже разбиралась в «Кванте» (М207, решение — «Квант», 1974, № 2).