Условие задачи (1979, № 5) Задача М564 // Квант. — 1979. — № 5. — Стр. 22—23; 1980. — № 4. — Стр. 33.
Для каких точек
- центрами окружностей, описанных соответственно около треугольников
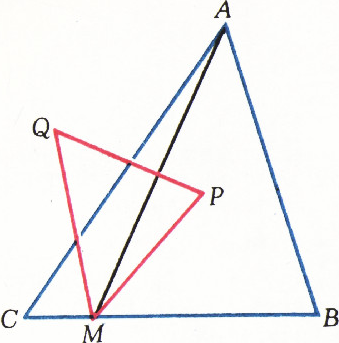
$ABM$ и$ACM$ (рис. 1); - точками пересечения их медиан;
- точками пересечения их высот?
Изображения страниц
Решение задачи (1980, № 4) Задача М564 // Квант. — 1979. — № 5. — Стр. 22—23; 1980. — № 4. — Стр. 33.
а) Покажем, что точку
Треугольники
Вокруг каждого из четырёхугольников
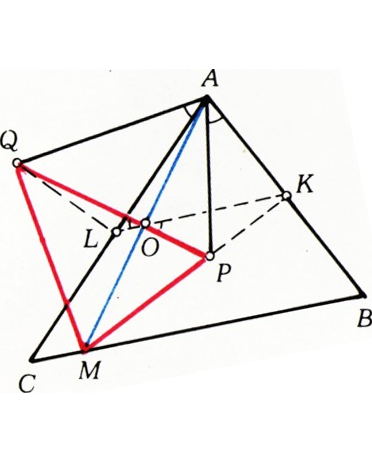
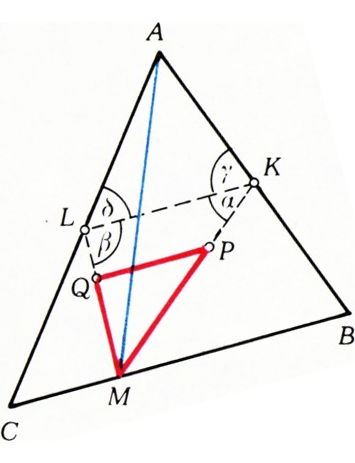
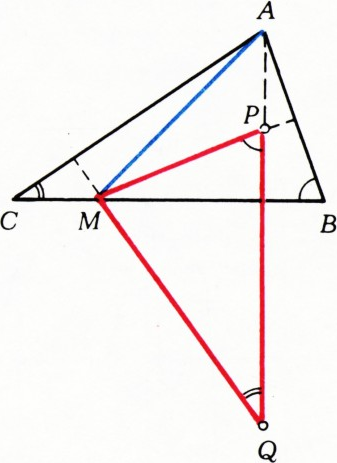
б) Гомотетия с коэффициентом
$\alpha = \delta$ (см. рис. 2); тогда$(AL)\parallel(KM)$, так что$|MB|=|MC|$, т. е.$M$ — середина$BC$. $\alpha=\gamma$; тогда$(AM)\perp(KL)$, так что$M$ — проекция вершины$A$ на сторону$BC$. $\alpha=\widehat A$; тогда либо$\beta=\gamma$ и$|MB|=|MC|$, либо$\beta=\delta$ и$M$ — проекция вершины$A$ (на$[BC]$).
Нетрудно убедиться, что верно и обратное: если
в) В этом случае, как и в случае а), точку
К сожалению, при публикации условия этой задачи наборщик перепутал знаки подобия и конгруэнтности (он учился ещё по старой программе); мы приносим извинения читателям, которым эта опечатка помешала понять условие.


