Задача М563‍‍

Предположим, что утверждение задачи неверно, т. е. что во всех точках $x\in[a;b]$‍‍ выполнено неравенство $$ f'(x)-(f(x))^2\ge1, $$ или $$ \dfrac{f'(x)}{1+(f(x))^2}\ge1. $$

Поскольку $(\arctg y)'=\dfrac1{1+y^2}$‍,‍ слева стоит производная сложной функции $\mathit\Phi(x)=\arctg f(x)$‍.‍ Итак, мы знаем, что во всех точках отрезка $[a;b]$‍‍ $$ \mathit\Phi'(x)\ge1. $$

Воспользуемся формулой Ньютона‍—‍Лейбница: $$ \mathit\Phi(b)-\mathit\Phi(a)=\int\limits_a^b\mathit\Phi'(x)\,dx\ge\int\limits_a^bdx=b-a=4. $$

Но $\arctg$‍‍ принимает лишь значения из интервала $\left(-\dfrac\pi2;\dfrac\pi2\right)$‍‍ и значит, $\Phi(b)-\Phi(a)\lt\pi$‍.‍ Получили противоречие.

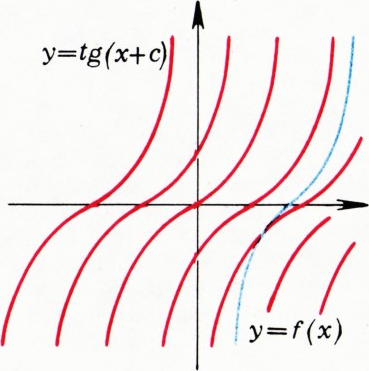
Из нашего решения ясно, что утверждение задачи верно для отрезка $[a;b]$‍‍ длины $\pi$‍‍ (или больше). Кроме того, в нашем решении мы нигде не пользовались непрерывностью производной функции $f$‍.‍

Наглядную интерпретацию задачи можно получить, заметив, что дифференциальное уравнение $\dfrac{y'}{1+y^2}=1$‍‍ имеет решение $y=\tg(x+c)$‍:‍ если в каждой точке $(x;y)$‍‍ график функции $f$‍‍ имеет наклон более крутой, чем график функции $y=\tg(x+c)$‍,‍ то $f$‍‍ нельзя продолжить на отрезок длины $\pi$‍‍ (см. рисунок) — график «уходит в бесконечность».