Условие задачи (1977, № 1) Задача М424 // Квант. — 1977. — № 1. — Стр. 26; 1977. — № 9. — Стр. 37.
Через каждую вершину тетраэдра проведена плоскость, содержащая центр окружности, описанной около противоположной грани, и перпендикулярная противоположной грани. Докажите, что эти четыре плоскости пересекаются в одной точке.
Изображения страниц
Решение задачи (1977, № 9) Задача М424 // Квант. — 1977. — № 1. — Стр. 26; 1977. — № 9. — Стр. 37.
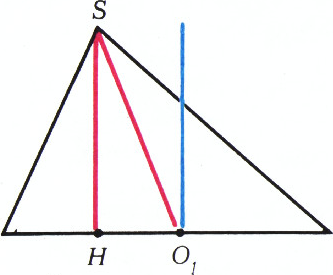
Пусть

