Условие задачи (1975, № 5) Задача М322 // Квант. — 1975. — № 5. — Стр. 50; 1976. — № 1. — Стр. 52—53.
- Фигура, состоящая более чем из одной точки, является пересечением
$N$ кругов. Докажите, что границу этой фигуры можно представить в виде объединения$2N - 2$ дуг окружностей. - В алфавите
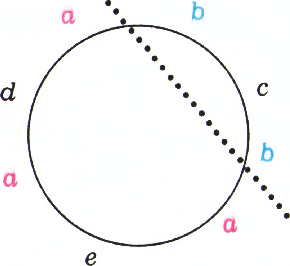
$N$ букв. Несколько букв выписано по окружности так, что никакая буква не встречается два раза подряд и для любых двух различных букв a, b можно провести прямую так, что все буквы a будут по одну сторону от прямой, а буквы b — по другую (рис. 1). Докажите, что выписано не более$2N-2$ букв.
Изображения страниц
Решение задачи (1976, № 1) Задача М322 // Квант. — 1975. — № 5. — Стр. 50; 1976. — № 1. — Стр. 52—53.
Текстовое представление решения задачи находится в процессе подготовки. С графическим представлением можно ознакомиться в опубликованном номере


