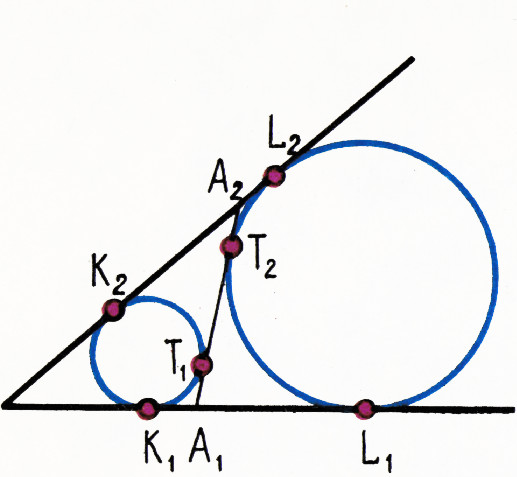
а) В угол вписаны две окружности; у них есть общая внутренняя касательная $T_1 T_2$ ($T_1$ и $T_2$ — точки касания), которая пересекает стороны угла в точках $A_1$ и $A_2$. Докажите что $A_1 T_1=A_2 T_2$ (или, что эквивалентно, $A_1 T_2=A_2 T_1$).
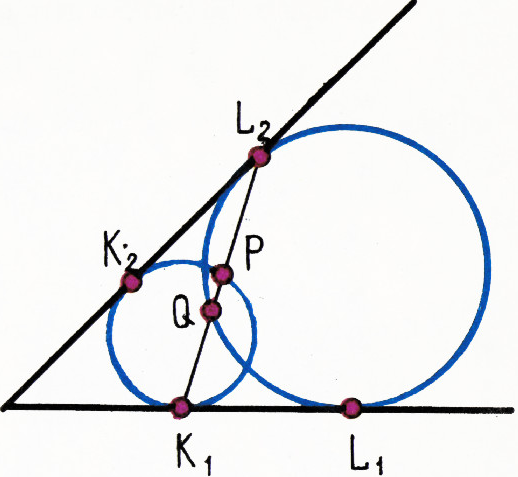
б) В угол вписаны две окружности, одна из них касается сторон угла в точках $K_1$ и $K_2$, другая — в точках $L_1$ и $L_2$. Докажите, что прямая $K_1 L_2$ высекает на этих двух окружностях равные хорды.
а) Можно считать, что точки $T_1$ и $T_2$ лежат на прямой $A_1A_2$, в таком порядке: $A_1$, $T_1$, $T_2$, $A_2$ (рис. 2). Тогда, поскольку
две касательные, проведённые из одной точки к окружности, равны, имеем
$$
A_1T_1=A_1K_1,\quad A_1T_2=A_1L_1,\quad A_2T_2=A_2L_2,\quad
A_2T_1=A_2K_2,\quad K_2L_2=K_1L_1,
$$
откуда
$$
A_1T_1+A_1T_2=A_2T_1+A_2T_2,\quad 2A_1T_1+T_1T_2=2A_2T_2+T_1T_2,\quad
A_1T_1=A_2T_2.
$$
Рис. 2Рис. 3
б) Пусть $P$ — точка пересечения $K_1L_2$ с окружностью, касающейся
сторон угла в точках $K_1$ и $K_2$; $Q$ — точка пересечения $K_1L_2$ со второй окружностью (рис. 3). Воспользуемся тем, что квадрат касательной
равен произведению отрезков секущей, проведённой из той же точки:
$$
L_1K_1^2=K_1Q\cdot K_1L_2,\quad L_2K_2^2=L_2P\cdot L_2K_1.
$$
Поскольку $L_1K_1=L_2K_2$, получаем $K_1Q\cdot K_1L_2=L_2P\cdot L_2K_1$,
откуда $K_1Q=L_2P$.
Прибавив к обеим частям этого равенства $PQ$ (или, в зависимости от порядка расположения точек $P$ и $Q$ на отрезке $K_1L_2$, отняв $PQ$ от обеих частей равенства), получим требуемое: $K_1P=L_2Q$.
Близкое к этому решение прислали А. Вировлянский из Горького и Д. Григорьев.
