а) Докажите, что для любой точки $M$ окружности, описанной около
правильного треугольника $ABC$, один из трёх отрезков $MA$, $MB$, $MC$
равен сумме двух других.
б) Три равные окружности $\gamma_1$, $\gamma_2$, $\gamma_3$ попарно
касаются друг друга, и вокруг них описана окружность $\gamma$, которая
касается всех трёх: $\gamma_1$, $\gamma_2$ и $\gamma_3$. Докажите, что для любой точки $M$ окружности $\gamma$ касательная, проведённая из точки $M$
к одной из трёх окружностей $\gamma_1$, $\gamma_2$, $\gamma_3$ равна
сумме касательных, проведённых из точки $M$ к двум другим окружностям.
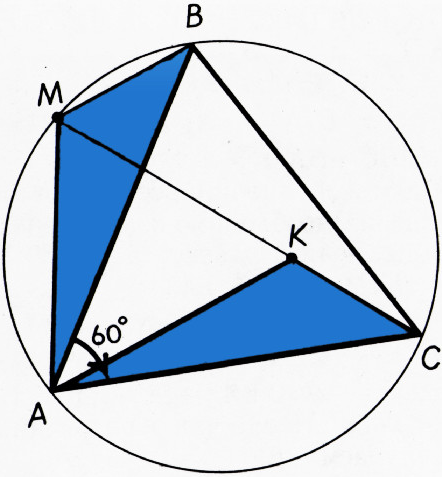
а) Пусть точка $M$ лежит на дуге $AB$ описанной окружности. Повернём
треугольник $AMB$ вокруг точки $A$ на $60^\circ$ так, чтобы он занял
положение $AKC$ (рис. 3). Поскольку углы $MBA$ и $MCA$ равны (они
опираются на одну и ту же дугу $AM$), точка $K$ лежит на отрезке $MC$.
Поскольку $AM=AK$ и $\angle MAK=60^\circ$ (по построению), треугольник $AMK$
равносторонний, поэтому $MK=AM$. Итак,
$$
MA+MB=MK+KC=MC.
$$
Другое решение получается сразу из теоремы Птолемея, согласно которой в любом вписанном четырёхугольнике произведение диагоналей равно сумме
произведений противоположных сторон: если в равенстве
$$
MC\cdot AB=MA\cdot BC + MB\cdot AC
$$
заменить $BC$ и $AC$ на $AB$, то получим
$$
MC\cdot AB=(MA+MB)AB
$$
откуда $MC=MA+MB$.
Эту задачу решили многие наши читатели. А. Браверман из Перми, А. Веселов из Калининской области,
В. Метлицкий из Ангарска, Н. Миролюбова из Актюбинска, О. Худавердян из Еревана прислали даже по несколько решений.
б) Докажем более общий факт. Пусть центры трёх окружностей радиуса $r$
являются вершинами равностороннего треугольника $C_0C_1C_2$ и $O$ — центр
описанной около него окружности радиуса $a$. Тогда для любой точки $M$
окружности радиуса $R=a+r$ с центром $O$ касательная, проведённая из точки
$M$ к одной из двух окружностей радиуса $r$, равна сумме касательных,
проведённых из точки $M$ к двум другим окружностям. Заметим, что при $r=0$
получается результат задачи а).
Рис. 4
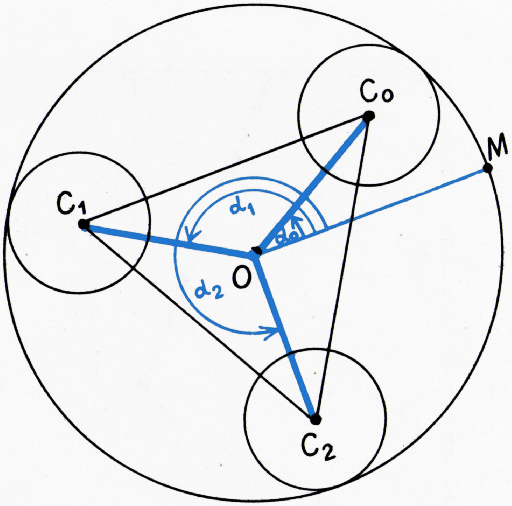
Пусть радиус $OM$ образует с радиусами $OC_k$ ($k=0$, 1, 2) углы
$\alpha_k=\alpha_0+k\cdot 120^\circ$ (рис. 4); тогда
$MC_k^2=R^2+a^2-2Ra\cos \alpha_k$, а квадрат касательной, проведённой из точки $M$ к соответствующей окружности, равен
$$
MC_k^2-r^2=R^2+a^2-2Ra\cos\alpha_k-(R-a)^2=2Ra(1-\cos\alpha_k).
$$
Поэтому касательные равны $2\sqrt{Ra}\sin\dfrac{\alpha_k}{2}$
($\sin\dfrac{\alpha_k}{2}\ge 0$, поскольку $0\le\alpha_k\lt2\pi$). Осталось
проверить равенство
$$
\sin\dfrac{\alpha_0}{2}+\sin\dfrac{\alpha_2}{2}=\sin\dfrac{\alpha_1}{2}.
$$
Это уже просто:
$$
\sin\dfrac{\alpha_0}{2}+\sin\dfrac{\alpha_2}{2}=2\cos60^\circ\cdot
\sin\dfrac{\alpha_0+\alpha_2}{4}=\sin\dfrac{\alpha_1}{2}.
$$
М. Прегер прислал решение этой задачи с помощью
аналитической геометрии. А. Браверман прислала нам интересное
доказательство (с помощью теоремы Птолемея) следующего обобщения задачи а):
пусть $M$ — точка на дуге $A_1A_{2n+1}$ окружности, описанной около
правильного $(2n+1)\text{-}$угольника $A_1A_2A_3\ldots A_{2n}A_{2n+1}$; тогда
$$
MA_1+MA_3+\ldots+MA_{2n+1}=MA_2+MA_4+\ldots+MA_{2n}.
$$
(Решение состоит в том, что выписываются равенства Птолемея для четырёхугольников $MA_1A_2A_3$, $MA_2A_3A_4$, $\ldots$,
$MA_{2n-1}A_{2n}A_{2n+1}$, $MA_{2n}A_{2n+1}A_{1}$, $MA_{2n+1}A_{2}A_{1}$,
причём все члены, содержащие $MA_{2k}$, помещаются в левой части равенства,
а все члены, содержащие $MA_{2k+1}$, — в правой, и затем все равенства
складываются.) Подумайте, как доказать это утверждение и аналогичное
обобщение задачи б) с помощью тригонометрических функций.
