Задача М1506‍‍

Докажем индукцией по $n$‍,‍ что существует разбиение отрезка $[a,b]$‍‍ на чёрные и белые кусочки, при котором суммы интегралов по чёрным и по белым кусочкам любого многочлена степени не выше $n$‍‍ равны.

Заметим, что достаточно доказать это для какого-то одного отрезка, скажем $[0;1]$‍,‍ поскольку при линейном преобразовании $x\to a+(b-a)x$‍‍ степень многочлена и свойства разбиения сохраняются.

При $n=1$‍‍ достаточно разбить отрезок на четыре равных кусочка, крайние объявить чёрными, а средние — белыми (рис. 1).

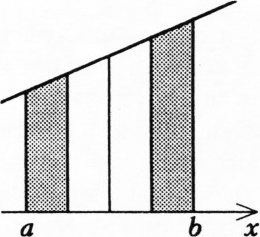
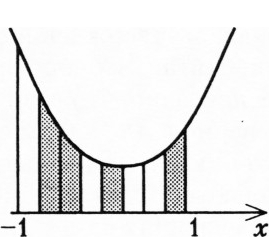
Предположив, что для многочленов степени $n-1$‍‍ утверждение доказано, рассмотрим многочлен степени $n$‍‍ $$ P_n(x)=ax^n+P_{n-1}(x) $$ на отрезке $[-1;1]$‍.‍ Разобьём отрезок $[0;1]$‍‍ так, как требуется для многочленов степени $n-1$‍,‍ а разбиение $[-1;0]$‍‍ возьмём симметричным ему относительно $0$‍,‍ если $n$‍‍ нечётно, и — симметричным с заменой цвета (чёрного на белый и обратно), если $n$‍‍ чётно (рис. 2). Тогда для $P_{n-1}(x)$‍‍ суммы интегралов равны на каждой половине $[-1;0]$‍‍ и $[0;1]$‍,‍ а для $ax^n$‍‍ сокращаются интегралы по кусочкам, симметричным относительно $0$‍.‍

Замечание. Конечно, индукцию можно начать и с $n=0$‍,‍ разбив отрезок пополам — на чёрный и белый.