Условие задачи (1994, № 6) Задача М1468 // Квант. — 1994. — № 6. — Стр. 20; 1995. — № 3. — Стр. 22—23.
Дан равнобедренный треугольник
$M$ — середина$BC$, и$O$ — точка на прямой$AM$ такая, что$OB$ и$AB$ перпендикулярны;$Q$ — произвольная точка отрезка$BC$, отличная от точек$B$ и$C$; - точка
$E$ лежит на прямой$AB$, точка$F$ лежит на прямой$AC$, и при этом точки$E$, $Q$ и$F$ различны и лежат на одной прямой.
Докажите, что
Изображения страниц
Решение задачи (1995, № 3) Задача М1468 // Квант. — 1994. — № 6. — Стр. 20; 1995. — № 3. — Стр. 22—23.
Вот одно из решений задачи чисто геометрическими средствами.
Предположим, что
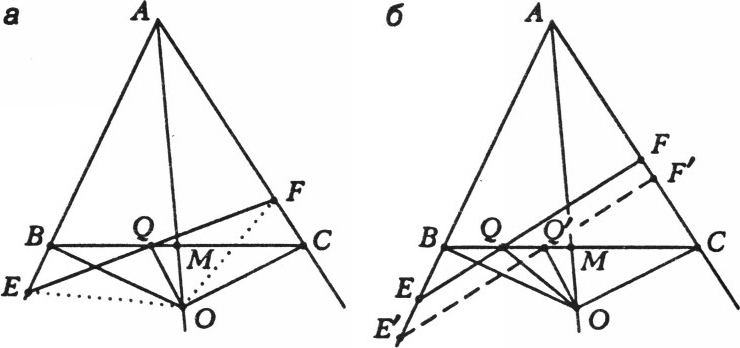
Предположим теперь, ЧТО
Замечание. Рисунок а — а именно, тот факт, что середина


