Задача М1373 / Задачи // Архив журнала «Квант»

Условие задачи (1992, № 11) Задача М1373 // Квант. — 1992. — № 11. — Стр. 18; 1993. — № 9/10. — Стр. 35.

Дана плоскость, пересекающая сферу с центром $O$‍‍ по окружности. На сфере по разные стороны от плоскости взяты точки $A$‍‍ и $B$‍,‍ причём радиус $OA$‍‍ перпендикулярен данной плоскости. Через прямую $AB$‍‍ проводится произвольная плоскость. Она пересекает окружность в точках $X$‍‍ и $Y$‍.‍ Докажите, что произведение $BX\cdot BY$‍‍ не зависит от выбора такой плоскости.

Б. Чиник

Межреспубликанская математическая олимпиада 1992 года

Открыть в номере

Изображения страниц

‍

Скачать PDF

Решение задачи (1993, № 9/10) Задача М1373 // Квант. — 1992. — № 11. — Стр. 18; 1993. — № 9/10. — Стр. 35.

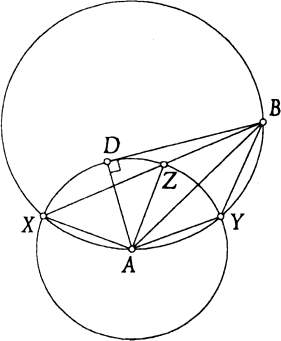
Сечением сферы плоскостью, проходящей через $AB$‍,‍ является окружность, содержащая точки $A$‍,‍ $B$‍,‍ $X$‍,‍ $Y$‍,‍ причём величины $AB=a$‍,‍ $AX=AY=b$‍‍ не зависят от выбора плоскости и $\angle ABX=\angle ABY$‍‍ (см. рисунок). Проведём окружность с центром $A$‍‍ и радиусом $b$‍.‍ Она пересечёт больший из отрезков $BX$‍,‍ $BY$‍,‍ скажем $BX$‍,‍ в некоторой точке $Z$‍,‍ удовлетворяющей равенству $BZ=BY$‍‍ (если $BX=BY$‍,‍ то $Z=X$‍).‍ Пусть $BD$‍‍ — касательная к этой окружности. Тогда $$ BX\cdot BY=BX\cdot BZ=BD^2=AB^2-AD^2=a^2-b^2 $$ — величина постоянная.

Б. И. Чиник

Открыть в номере

Метаданные Задача М1373 // Квант. — 1992. — № 11. — Стр. 18; 1993. — № 9/10. — Стр. 35.

Предмет

Математика

Условие

Чиник Б. И.

Решение

Чиник Б. И.

Номера

1992. — № 11. — Стр. 18 [условие]

1993. — № 9/10. — Стр. 35 [решение]

Описание

Задача М1373 // Квант. — 1992. — № 11. — Стр. 18; 1993. — № 9/10. — Стр. 35.

Ссылка

https://www.kvant.digital/problems/m1373/