Задача М1356 / Задачи // Архив журнала «Квант»

Условие задачи (1992, № 8) Задача М1356 // Квант. — 1992. — № 8. — Стр. 29; 1993. — № 1/2. — Стр. 35.

Докажите, что если $abc=4Rrr_c$‍,‍ где $a$‍,‍ $b$‍,‍ $c$‍‍ — стороны треугольника, $R$‍,‍ $r$‍,‍ $r_c$‍‍ — радиусы описанной, вписанной и одной из вневписанных окружностей, то треугольник прямоугольный. (Вневписанная окружность касается стороны $c$‍‍ и продолжений двух других сторон.)

Б. Турешбаев, ученик 11 класса

Открыть в номере

Изображения страниц

‍

Скачать PDF

Решение задачи (1993, № 1/2) Задача М1356 // Квант. — 1992. — № 8. — Стр. 29; 1993. — № 1/2. — Стр. 35.

Воспользуемся формулами $S=\dfrac{abc}{4R}$‍,‍ $S=rp$‍,‍ где $S$‍‍ — площадь треугольника, $p$‍‍ — его полупериметр.

Получаем: $p=r_c$‍.‍

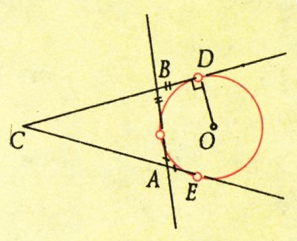
Отсюда, пользуясь равенством касательных, проведённых к окружности из одной точки, получаем (см. рисунок): $CD=OD$‍.‍ Значит, $\angle DCO=\dfrac\pi4$‍,‍ $\angle DCE=2\angle DCO=\dfrac\pi2$‍.‍

Б. Турешбаев

Открыть в номере

Метаданные Задача М1356 // Квант. — 1992. — № 8. — Стр. 29; 1993. — № 1/2. — Стр. 35.

Предмет

Математика

Условие

Турешбаев Б.

Решение

Турешбаев Б.

Номера

1992. — № 8. — Стр. 29 [условие]

1993. — № 1/2. — Стр. 35 [решение]

Описание

Задача М1356 // Квант. — 1992. — № 8. — Стр. 29; 1993. — № 1/2. — Стр. 35.

Ссылка

https://www.kvant.digital/problems/m1356/