Задача М1332‍‍

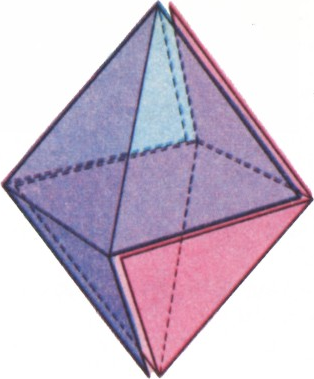
Ответ: 6. Легко изготовить правильный октаэдр из двух тетраэдров, у каждого из которых разрезаны три ребра, выходящих из одной вершины (основания этих тетраэдров будут служить противоположными гранями октаэдра, как показано на рисунке).

С другой стороны, меньшим числом разрезов обойтись нельзя. Ведь к каждой вершине октаэдра должно подходить не менее двух склеенных рёбер: если к какой-то вершине $A$‍‍ примыкало бы лишь одно такое ребро, то все примыкающие к $A$‍‍ четыре треугольника должны были бы принадлежать одному тетраэдру (их углы с вершиной $A$‍‍ вместе составляли бы в сумме $4\cdot60^\circ=240^\circ$‍),‍ а к вершине тетраэдра примыкают лишь три грани (с суммой углов $180^\circ$‍).‍ Поскольку у октаэдра шесть вершин, то концов у склеенных рёбер должно быть не менее $6\cdot2$‍,‍ а значит, этих рёбер — не менее 6.

Более интересный вопрос: можно ли склеить из 5 правильных тетраэдров, разрезанных по рёбрам, поверхность правильного икосаэдра — 20-гранника, в каждой вершине которого сходится по 5 треугольников, и если можно, то сколько рёбер для этого нужно разрезать. Если выясните — напишите нам об этом.