Задача М1331 / Задачи // Архив журнала «Квант»

Условие задачи (1992, № 3) Задача М1331 // Квант. — 1992. — № 3. — Стр. 18; 1992. — № 9. — Стр. 29.

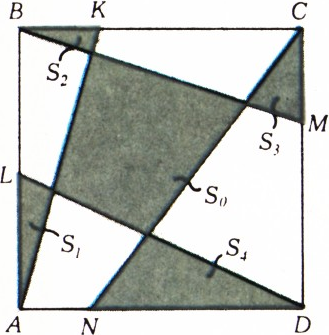
Отрезки $AK$‍,‍ $BM$‍,‍ $CN$‍,‍ $DL$‍‍ делят квадрат $ABCD$‍‍ со стороной 1 на четыре треугольника с площадями $S_1$‍,‍ $S_2$‍,‍ $S_3$‍,‍ $S_4$‍‍ и пять четырёхугольников (рис. 1); площадь центрального четырёхугольника равна $S_0$‍,‍ причём $S_0=S_1+S_2+S_3+S_4$‍.‍ Докажите равенство $$ AL+BK+CM+DN=2. $$

С. Сефибеков

Открыть в номере

Изображения страниц

‍

Скачать PDF

Решение задачи (1992, № 9) Задача М1331 // Квант. — 1992. — № 3. — Стр. 18; 1992. — № 9. — Стр. 29.

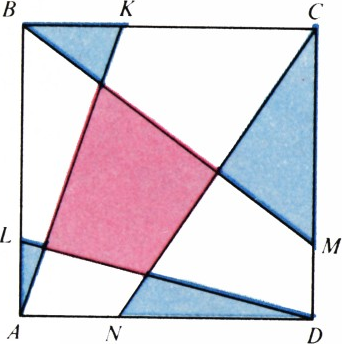
Разность между суммой площадей четырёх треугольников $DAL$‍,‍ $ABK$‍,‍ $BCM$‍,‍ $CDN$‍‍ и площадью квадрата равна разности между суммой площадей голубых треугольников и розового четырёхугольника, т. е. по условию она равна 0: $$ S_1+S_2+S_3+S_4-S_0=0. $$ Записывая площадь каждого из четырёх треугольников $DAL$‍,‍ $ABK$‍,‍ $BCM$‍,‍ $CDN$‍‍ как половину произведения катетов (один из катетов — сторона квадрата, равная 1), получим требуемое равенство: $$ \dfrac{AL}2+\dfrac{BK}2+\dfrac{CM}2+\dfrac{DN}2=1. $$

Заметим, что аналогичное утверждение будет справедливо также, если вместо квадрата $ABCD$‍‍ рассмотреть ромб (поскольку у ромба все высоты равны).

С. Сефибеков

Открыть в номере

Метаданные Задача М1331 // Квант. — 1992. — № 3. — Стр. 18; 1992. — № 9. — Стр. 29.

Предмет

Математика

Условие

Сефибеков С.

Решение

Сефибеков С.

Номера

1992. — № 3. — Стр. 18 [условие]

1992. — № 9. — Стр. 29 [решение]

Описание

Задача М1331 // Квант. — 1992. — № 3. — Стр. 18; 1992. — № 9. — Стр. 29.

Ссылка

https://www.kvant.digital/problems/m1331/