Задача М1224‍‍

Ответ: a), в) не может, б) может.

Введём обозначения, как на рисунке. Заметим, что если длины двух крайних частей проведённого отрезка $AD$‍‍ равны ($AN=DM$‍),‍ то треугольник $ABD$‍,‍ очевидно, равнобедренный ($AB=BD$‍).‍ Следовательно, $AD$‍‍ не может быть ни высотой ($\angle ADB\lt90^\circ$‍),‍ ни биссектрисой ($\angle CAD\lt\angle ADB=\angle BAD$‍),‍ а медианой он может являться лишь тогда, когда $a=2c$‍,‍ где $a=BC$‍,‍ $c=AB$‍.‍

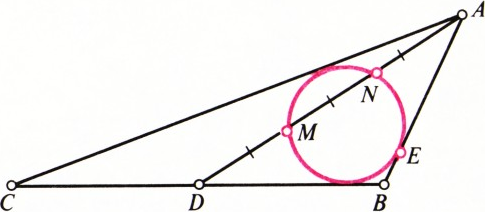
Пусть теперь условие $a=2c$‍‍ выполнено. Покажем, что при некотором $b=AC$‍‍ вписанная окружность поделит медиану $AD=m$‍‍ на равные части. Нам понадобятся следующие три хорошо известные и очень полезные утверждения:

1. $$m^2=\dfrac{2b^2+2c^2-a^2}4;$$
2. $$AE=\dfrac{b+c-a}2,$$ где $E$‍‍ — точка касания вписанной окружности со стороной $AB$‍;‍
3. $$AE^2=AN\cdot AM$$ (это верно для любой секущей $ANM$‍).‍

Подставляя в равенства 1) и 2) $a=2c$‍,‍ в 3) — значение $AE$‍‍ из 2), $AN=\dfrac m3$‍,‍ $AM=\dfrac{2m}3$‍‍ и $m^2$‍‍ из 1), получим условие $$ AE^2=\left(\dfrac{b-c}2\right)^2=\dfrac29m^2=\dfrac29\,\dfrac{b^2-c^2}2, $$ или $9(b-c)=4(b+c)$‍‍ (сокращение на $b-c$‍‍ возможно, так как $a=2c\lt b+c$‍,‍ т. е. $b-c\gt0$‍).‍ Отсюда $b=\dfrac{13}5c$‍.‍ Поскольку $2c-c\lt\dfrac{13}5c\lt2c+c$‍,‍ треугольник со сторонами $2c$‍,‍ $\dfrac{13}5c$‍,‍ $c$‍‍ существует. Части $AN$‍‍ и $DM$‍‍ медианы в таком треугольнике равны, так как $BD=c=BA$‍.‍ Отрезок $x=AN$‍‍ удовлетворяет уравнению $x(m-x)=AN\cdot AM=AE^2=\dfrac29m^2$‍,‍ имеющему корни $\dfrac m3$‍‍ и $\dfrac{2m}3$‍,‍ и неравенству $x\lt m-x$‍‍ ($AN\lt AM$‍).‍ Следовательно, $x=\dfrac m3$‍,‍ что нам и требовалось.