Условие задачи (1988, № 11/12) Задача М1140 // Квант. — 1988. — № 11/12. — Стр. 34; 1989. — № 5. — Стр. 33—34.
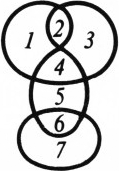
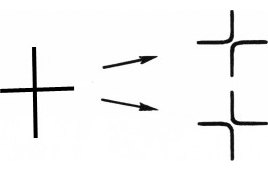
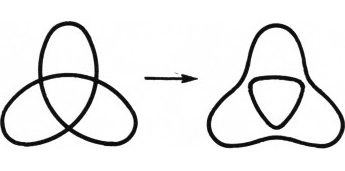
Нарисуем на плоскости одну или несколько пересекающихся кривых (кривые могут иметь точки самопересечения, рис. 1). В каждой точке пересечения можно двумя способами выполнить «перестройку» (рис. 2). Если проделать перестройку во всех точках пересечения, то получится несколько непересекающихся кривых (рис. 3).
- Докажите, что число непересекающихся кривых, которые могут получиться, не больше числа областей, на которые делили плоскость исходные кривые (на рисунке 1 таких областей 7).
- Всегда ли можно сделать перестройки так, чтобы в результате получалась одна кривая?
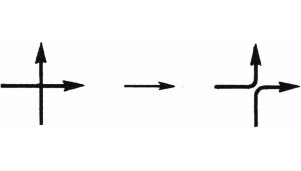
- Выберем на каждой кривой направление обхода и будем производить перестройки в соответствии с этими направлениями так, чтобы стрелки «отталкивались» друг от друга (рис. 4). Может ли в результате получиться одна кривая?
Изображения страниц
Решение задачи (1989, № 5) Задача М1140 // Квант. — 1988. — № 11/12. — Стр. 34; 1989. — № 5. — Стр. 33—34.
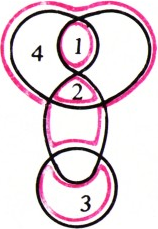
а) Пусть первоначально данные кривые делили плоскость на области
б) Раскрасим исходную картинку в шахматном порядке, т. е. так, чтобы внешняя область была белой и цвет области менялся при переходе через границу (рис. 6, а). (Существование такой раскраски легко доказать по индукции. При добавлении к уже раскрашенной картинке одной несамопересекающейся замкнутой кривой все попавшие внутрь неё области или отрезаемые этой кривой от старых областей части перекрашиваются в другой цвет; внешняя раскраска сохраняется. При этом шахматный порядок цветов не нарушится. А любую замкнутую кривую можно разбить на несамопересекающиеся замкнутые куски.)
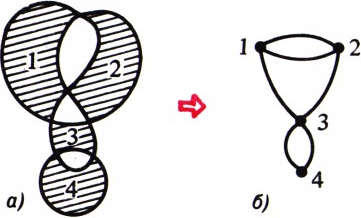
Построим по «шахматной раскраске» граф (рис. 6, б), сопоставив каждой чёрной области по одной точке — это будут вершины графа, а каждой точке пересечения кривых — одно ребро: оно соединяет вершины, отвечающие чёрным областям, которые примыкают к этой точке.
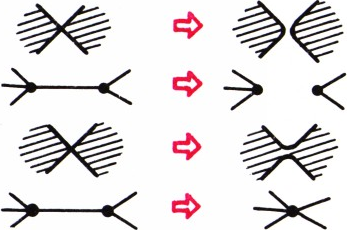
Два способа перестройки изображаются на графе двумя операциями: стиранием ребра и стягиванием ребра в точку (рис. 7).
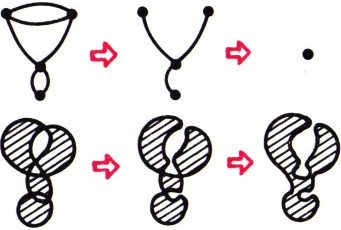
Ясно, что на графе исходной картинки можно стереть часть ребер так, что он превратится в «дерево», т. е. граф, не имеющий замкнутых цепочек рёбер. Оставшиеся рёбра можно последовательно стянуть в точку. Соответствующая последовательность перестроек приводит к одной чёрной области. Её граница и есть искомая кривая (рис. 8).
Интересно, что по графу можно восстановить соответствующий набор кривых. Подумайте, например, какие кривые отвечают графам, изображённым на рисунке 9.
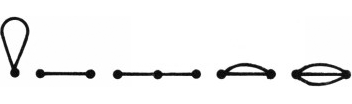

в) Каждая перестройка превращает набор ориентированных кривых снова в набор ориентированных кривых. Предположим, что существует последовательность перестроек, результатом которой будет единственная кривая. Тогда перед выполнением последней перестройки мы располагаем набором ориентированных кривых с единственной точкой пересечения. Такой набор может состоять из единственной кривой — «восьмёрки», изображённой на рисунке 10. Однако её перестройка приводит к двум, а не к одной кривой.


