Условие задачи (1988, № 5) Задача М1103 // Квант. — 1988. — № 5. — Стр. 29; 1988. — № 9. — Стр. 43—44.
- На бесконечной плоскости, разбитой на квадратные клетки, некоторое — быть может бесконечное — количество прямоугольников размером
$1\times2$ закрашены в чёрный цвет так, что никакие два чёрных прямоугольника не имеют общих точек (даже вершин). Докажите, что оставшуюся часть плоскости можно замостить этими прямоугольниками. - Пусть на клетчатой плоскости закрашены несколько прямоугольников размером
$m\times n$, не имеющих общих точек. Докажите, что если$mn$ чётно, то оставшуюся часть плоскости можно замостить прямоугольниками размером$1\times2$, а если$mn$ — нечётно, то это не всегда возможно.
Изображения страниц
Решение задачи (1988, № 9) Задача М1103 // Квант. — 1988. — № 5. — Стр. 29; 1988. — № 9. — Стр. 43—44.
Покроем исходную (голубую) клетчатую сетку более крупной (чёрной), разбивающей плоскость на квадраты
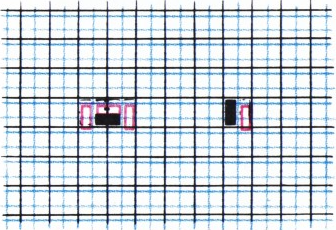
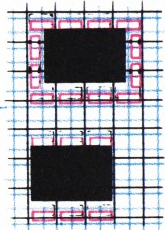
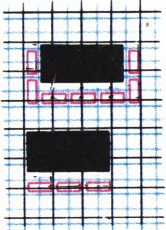
Аналогично, с помощью сетки из квадратов
Докажем теперь, что если
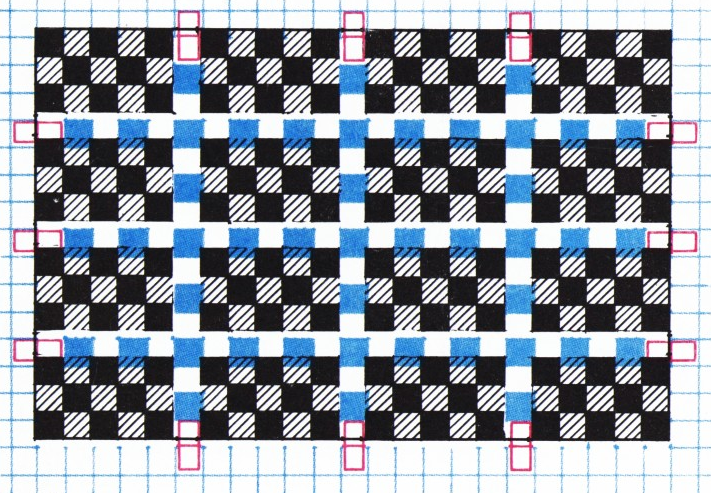
Пусть
Предположим, что вся эта область покрыта домино. Некоторые из них — но не более


