Условие задачи (1988, № 2) Задача М1087 // Квант. — 1988. — № 2. — Стр. 26; 1988. — № 6. — Стр. 28—29.
Рассмотрим треугольник
- существует одна и только одна точка
$M$, для которой отрезки$AA_1$, $BB_1$ и$CC_1$ равны; - для такой точки
$M$ длины отрезков$AA_1$, $BB_1$, $CC_1$ равны диаметру вписанной в треугольник$ABC$ окружности.
Изображения страниц
Решение задачи (1988, № 6) Задача М1087 // Квант. — 1988. — № 2. — Стр. 26; 1988. — № 6. — Стр. 28—29.
а), б) Проведём через каждую вершину треугольника
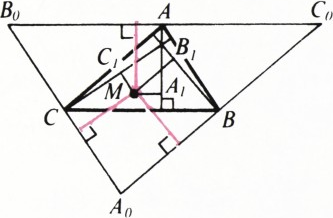
Найденная выше точка


