Задача М1079‍‍

Ответ: можно; искомыми точками являются, например, точки $P_i(i;i^2)$‍,‍ $i=1$‍,‍ 2, $\ldots$‍,‍ $n$‍,‍ т. е. точки на параболе $y=x^2$‍‍ с натуральными абсциссами.

В самом деле, $$ P_iP_j=\sqrt{(j-i)^2+(j^2-i^2)^2}=|j-i|\sqrt{1+(j+i)^2}. $$ Но число вида $1+m^2$‍‍ (у нас $m=j+i$‍)‍ не может быть квадратом рационального числа $r$‍,‍ потому что в таком случае $r$‍‍ было бы натуральным и из равенства $r^2=1+m^2$‍‍ получалось бы противоречивое неравенство: $$ 1=r^2-m^2=(r-m)(r+m)\ge r+m\gt1. $$ Таким образом, все расстояния $P_iP_j$‍‍ иррациональны.

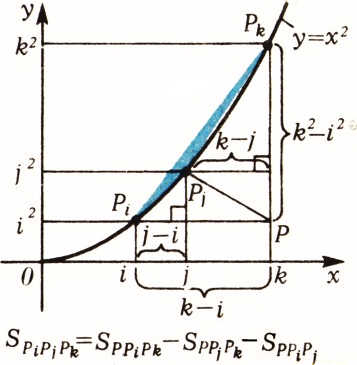
В то же время площадь треугольника $P_iP_jP_k$‍‍ при $i\lt j\lt k$‍,‍ как видно из рисунка, равна $$ \dfrac12((k-i)(k^2-i^2)-(k-j)(k^2-i^2)-(k-i)(j^2-i^2)), $$ т. е. рациональна.

Вообще, площадь любого треугольника, вершины которого имеют целые координаты, рациональна. Это показывает, что условия задачи легко выполнимы: можно брать любой набор точек целочисленной решётки, заботясь лишь о том, чтобы расстояния между ними были иррациональны.